题目内容
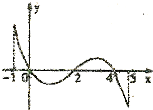 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 1.5 | 2 | 1 |
②函数f(x)在[0,2]上是减函数;
③当1<a<2时,函数y=f(x)-a最多有4个零点;
④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4.
其中正确命题的序号是
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:通过函数的图象,再结合表格可直接读出.
解答:
解:①由图象得:f(0),f(4)是极大值,而f(2)是极小值,f(-1),f(5)是端点值,
∴最大值在f(0),f(4),f(-1)中取,最小值在f(2),f(5)中取;
结合表格得:①正确.
②由图象得:在[0,2]上,f′(x)<0,∴f(x)是减函数,故②正确.
③画出函数y=f(x)-a的草图,可以发现,
当a=1.5时,有三个零点,当a=2时有两个零点,当1.5<a<2时,有4个零点,故③正确.
④由图象得函数f(x)的定义域[-1,5],f(x)的最大值是2,t的最大值是5.
故答案为:①②③.
∴最大值在f(0),f(4),f(-1)中取,最小值在f(2),f(5)中取;
结合表格得:①正确.
②由图象得:在[0,2]上,f′(x)<0,∴f(x)是减函数,故②正确.
③画出函数y=f(x)-a的草图,可以发现,
当a=1.5时,有三个零点,当a=2时有两个零点,当1.5<a<2时,有4个零点,故③正确.
④由图象得函数f(x)的定义域[-1,5],f(x)的最大值是2,t的最大值是5.
故答案为:①②③.
点评:本题考察了函数的单调性,极值,导数的应用,以及读图的能力.

练习册系列答案
相关题目
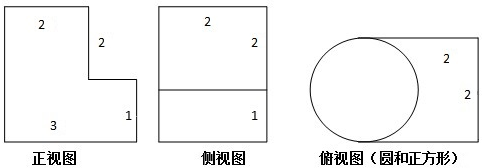
 在三棱锥D-ABC中,AC=BC=CD=2,CD⊥平面ABC,∠ACB=90°.若其主视图,俯视图如图所示,则其左视图的面积为
在三棱锥D-ABC中,AC=BC=CD=2,CD⊥平面ABC,∠ACB=90°.若其主视图,俯视图如图所示,则其左视图的面积为