题目内容
如果双曲线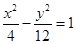 上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( )
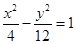 上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( ) | A.4 | B.12 | C.4或12 | D.不确定 |
C
试题分析:因为双曲线上的点到双曲线焦点的距离之差的绝对值为定值,且双曲线
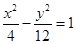 上一点P到它的右焦点距离是8,所以点P到它的左焦点的距离是2×2+8=12或8-2×2=4,故选C。
上一点P到它的右焦点距离是8,所以点P到它的左焦点的距离是2×2+8=12或8-2×2=4,故选C。点评:简单题,双曲线上的点到双曲线焦点的距离之差的绝对值为定值。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
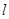 经过抛物线
经过抛物线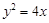 的焦点F,且与抛物线相交于A、B两点.
的焦点F,且与抛物线相交于A、B两点.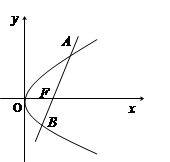
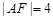 ,求点A的坐标;
,求点A的坐标; ,求线段AB的长.
,求线段AB的长.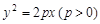 的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若
的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若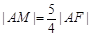 ,则
,则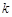 的值 .
的值 .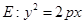 ,在抛物线上任意画一个点
,在抛物线上任意画一个点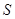 ,度量点
,度量点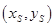 ,如图.
,如图.
 时,
时,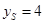 ,试求抛物线
,试求抛物线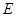 的方程;
的方程;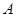 ,焦点为
,焦点为 ,构造直线
,构造直线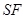 交抛物线
交抛物线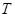 ,构造直线
,构造直线 、
、 分别交准线于
分别交准线于 、
、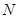 两点,构造直线
两点,构造直线 、
、 .经观察得:沿着抛物线
.经观察得:沿着抛物线 .请你证明这一结论.
.请你证明这一结论. 
 ”,其余条件不变,发现“
”,其余条件不变,发现“ 倍
倍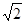 倍
倍 倍
倍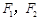 ,过
,过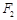 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点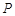 ,
,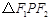 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )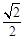

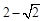
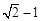
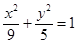 的中心为顶点,右焦点为焦点的抛物线方程是 .
的中心为顶点,右焦点为焦点的抛物线方程是 .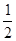 ,
,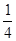 )处的切线的倾斜角是( )
)处的切线的倾斜角是( )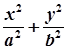 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.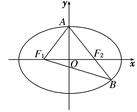
 =2
=2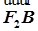 ,
,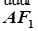 ·
·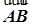 =
=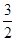 ,求椭圆的方程.
,求椭圆的方程.