题目内容
已知抛物线C: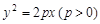 的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若
的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若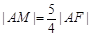 ,则
,则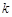 的值 .
的值 .
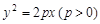 的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若
的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若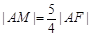 ,则
,则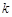 的值 .
的值 .
试题分析:根据题意设直线AB的方程为y=
 ,则与抛物线
,则与抛物线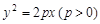 联立,可知交点A,B的坐标关系,然后结合抛物线的定义可知若
联立,可知交点A,B的坐标关系,然后结合抛物线的定义可知若 等于点A到其准线的距离,那么转化可知直线倾斜角的余弦值为
等于点A到其准线的距离,那么转化可知直线倾斜角的余弦值为 ,则可知直线AB的斜率k为
,则可知直线AB的斜率k为 ,故答案为
,故答案为 。
。点评:解决的关键是利用直线与抛物线的位置关系结合抛物线的定义和性质来解得,属于基础题。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
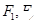 是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引
是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引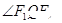 的平分线的垂线,垂足为P,则点P的轨迹是
的平分线的垂线,垂足为P,则点P的轨迹是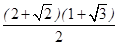
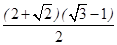
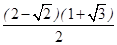
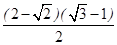
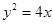 上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )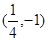
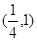
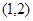
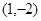
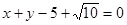 ;l2:
;l2: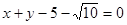 均相切.
均相切.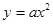 上一点M,作圆C的一条切线ME,切点为E,且
上一点M,作圆C的一条切线ME,切点为E,且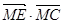 的最小值为4,求此抛物线准线的方程.
的最小值为4,求此抛物线准线的方程.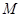 ,两个焦点为
,两个焦点为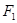 、
、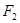 ,
,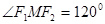 ,则双曲线的离心率为____________.
,则双曲线的离心率为____________.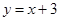 与曲线
与曲线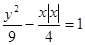 的交点的个数是 个.
的交点的个数是 个.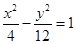 上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( ) 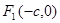 、
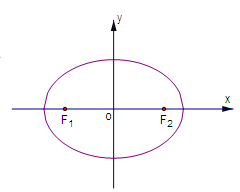
、 分别是椭圆
分别是椭圆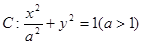 的左、右焦点,
的左、右焦点,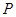 为椭圆
为椭圆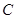 上任意一点,且
上任意一点,且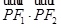 最小值为
最小值为 .
.
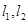 均与椭圆
均与椭圆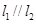 ,试探究在
,试探究在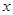 轴上是否存在定点
轴上是否存在定点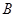 ,点
,点