题目内容
6.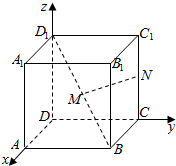 如图所示,建立空间直角坐标系Dxyz,已知正方体ABCD-A1B1C1D1的棱长为1,点M是正方体对角线D1B的中点,点N在棱CC1上.
如图所示,建立空间直角坐标系Dxyz,已知正方体ABCD-A1B1C1D1的棱长为1,点M是正方体对角线D1B的中点,点N在棱CC1上.(1)当2|C1N|=|NC|时,求|MN|;
(2)当点N在棱CC1上移动时,求|MN|的最小值并求此时的N点坐标.
分析 (1)求出M($\frac{1}{2},\frac{1}{2},\frac{1}{2}$),N(0,1,$\frac{2}{3}$),由此能求出|MN|.
(2)当MN是BD1和CC1的公垂线时,|MN|取最小值,由此得到当N是CC1中点时,|MN|取最小值.
解答 解:(1)∵如图所示,建立空间直角坐标系Dxyz,
正方体ABCD-A1B1C1D1的棱长为1,点M是正方体对角线D1B的中点,
点N在棱CC1上,2|C1N|=|NC|,
∴D1(0,0,1),B(1,1,0),M($\frac{1}{2},\frac{1}{2},\frac{1}{2}$),N(0,1,$\frac{2}{3}$),
∴|MN|=$\sqrt{(0-\frac{1}{2})^{2}+(1-\frac{1}{2})^{2}+(\frac{2}{3}-\frac{1}{2})^{2}}$=$\frac{\sqrt{19}}{6}$.
(2)∵点M是正方体对角线D1B的中点,点N在棱CC1上移动时,
∴当MN是BD1和CC1的公垂线时,|MN|取最小值,
∴当N是CC1中点时,|MN|取最小值,
此时N(0,1,$\frac{1}{2}$),|MN|min=$\sqrt{(0-\frac{1}{2})^{2}+(1-\frac{1}{2})^{2}+(\frac{1}{2}-\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查线段长的求法,考查两点间距离的最小值及相应的点的坐标的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
13.在△ABC中,cos(A+B)=( )
| A. | cosC | B. | -cosC | C. | sinC | D. | -sinC |
11.若函数f(x)满足f′(x)-f(x)=2xex,f(0)=1,其中f′(x)为f(x)的导函数,则当x>0时,$\frac{f′(x)}{f(x)}$的最大值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
15.已知椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中:
(1)求椭圆C1和抛物线C2的标准方程;
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点.
①求证:直线PA,PF,PB的斜率成等差数列;
②若点P在x轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点.
①求证:直线PA,PF,PB的斜率成等差数列;
②若点P在x轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
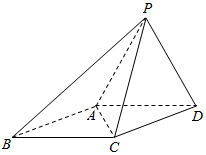 如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.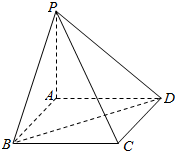 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.