题目内容
13.函数f(x)=$\sqrt{|x+1|+|x+2|-a}$.(Ⅰ)若a=5,求函数f(x)的定义域A;
(Ⅱ)设a,b∈(-1,1),证明:$\frac{|a+b|}{2}$<|1+$\frac{ab}{4}$|.
分析 (Ⅰ)把a=5代入,然后由根式内部的代数式大于等于0,求解绝对值的不等式得答案;
(Ⅱ)把要证的不等式转化为2|a+b|<|4+ab|,然后利用平方作差证得答案.
解答 (Ⅰ)解:由|x+1|+|x+2|-5≥0,得x≤-4或x≥1.
∴A={x|x≤-4或x≥1};
(Ⅱ)证明:∵$\frac{|a+b|}{2}<|1+\frac{ab}{4}|?2|a+b|<|4+ab|$,
而4(a+b)2-(4+ab)2=4(a2+2ab+b2)-(16+8ab+a2b2)
=4a2+4b2-a2b2-16=a2(4-b2)+4(b2-4)=(b2-4)(4-a2),
又∵a,b∈(-1,1),∴(b2-4)(4-a2)<0,
∴4(a+b)2<(4+ab)2,
故$\frac{|a+b|}{2}<|1+\frac{ab}{4}|$.
点评 本题考查函数的定义域及其求法,考查了绝对值不等式的解法,训练了利用作差法证明不等式,是中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
3.已知(1+ax)7的展开式中各项的系数之和为-1,则a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
1.设Sn、Tn分别为等差数列{an}与{bn}的前n项和,若$\frac{S_n}{T_n}=\frac{2n-1}{3n+2},则\frac{a_7}{b_7}$等于( )
| A. | $\frac{13}{23}$ | B. | $\frac{27}{44}$ | C. | $\frac{25}{41}$ | D. | $\frac{23}{38}$ |
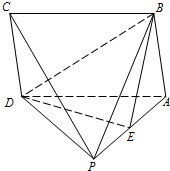 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E为侧棱PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E为侧棱PA的中点.