题目内容
三棱锥P-ABC的四个顶点在同一球面上,PA、PB、PC两两互相垂直,且这个三棱锥的三个侧面的面积分别为
,2
,
,则这个球的表面积是
| 2 |
| 3 |
| 6 |
9π
9π
.分析:三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,它的外接球就是它扩展为长方体的外接球,求出长方体的对角线的长就是球的直径,然后求球的表面积即可.
解答:解:∵三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,它的外接球就是它扩展为长方体的外接球
设PA=a,PB=b,PC=c则
∴①×②×③可得abc=2
④
∴④÷①得c=
④÷②得b=1
④÷③得a=
∴求出长方体的对角线的长:
=3
∴球的直径是3,半径为
∴球的表面积:4π(
)2=9π
故答案为9π
设PA=a,PB=b,PC=c则
|
∴①×②×③可得abc=2
| 3 |
∴④÷①得c=
| 6 |
④÷②得b=1
④÷③得a=
| 2 |
∴求出长方体的对角线的长:
(
|
∴球的直径是3,半径为
| 3 |
| 2 |
∴球的表面积:4π(
| 3 |
| 2 |
故答案为9π
点评:本题考查球的表面积,几何体的外接球,考查空间想象能力,计算能力,是基础题.解题的关键是要知道三棱锥P-ABC的四个顶点在同一球面上,PA、PB、PC两两互相垂直则球的直径是以PA,PB,PC所构造出的长方体得对角线长这一常用结论!

练习册系列答案
相关题目
 三棱锥P-ABC的四个顶点都在体积为
三棱锥P-ABC的四个顶点都在体积为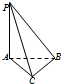 已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )
已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )