题目内容
已知三棱锥P-ABC中，△ABC是边长为3的等边三角形，侧棱长都相等，半径为2的球O过三棱锥P-ABC的四个顶点，则PA=
2或2
| 3 |
2或2
．| 3 |
分析：设P在底面的射影是E，延长AE交BC于D，连接PD、OA、OB、OC．因为△ABC是等边三角形且侧棱长都相等，所以三棱锥P-ABC是正三棱锥，因此Rt△AOE中算出OE=1，再在Rt△PAE中，运用勾股定理即可算出PA的长度．
解答：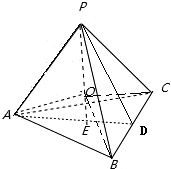
解：根据题意，三棱锥P-ABC是正三棱锥，设P在底面的射影是E
延长AE交BC于D，连接PD、OA、OB、OC
∵，△ABC是边长为3的等边三角形，
∴AE=
AB=
，DE=
∵半径为2的球O过三棱锥P-ABC的四个顶点，
∴球心O在PE上，设OE=x
则AO=
=2，得（
）2+x2=4，解得x=1（舍负）
∴PE=PO±OE=1或3
因此，Rt△PAE中，PA=
=2或2
故答案为：2或2
解：根据题意，三棱锥P-ABC是正三棱锥，设P在底面的射影是E延长AE交BC于D，连接PD、OA、OB、OC
∵，△ABC是边长为3的等边三角形，
∴AE=
| ||
| 3 |
| 3 |
| ||
| 6 |
∵半径为2的球O过三棱锥P-ABC的四个顶点，
∴球心O在PE上，设OE=x
则AO=
| AE2+OE2 |
| 3 |
∴PE=PO±OE=1或3
因此，Rt△PAE中，PA=
| AE2+PE2 |
| 3 |
故答案为：2或2
| 3 |
点评：本题给出正三棱锥的底面边长为3，求外接球半径为2时侧棱的长，着重考查了正棱锥的性质和球内接多面体的计算等知识，属于中档题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知三棱锥P-ABC中，PC⊥底面ABC，AB=BC，D、F分别为AC、PC的中点，DE⊥AP于E．
如图，已知三棱锥P-ABC，∠ACB=90°，CB=4，AB=20，D为AB中点，M为PB的中点，且△PDB是正三角形，PA⊥PC．
（2009•河西区二模）如图，已知三棱锥P-ABC中，PA⊥面ABC，其中正视图为Rt△PAC，AC=2
（2009•黄浦区二模）已知三棱锥P-ABC的棱长都是2，点D是棱AP上不同于P的点．