题目内容
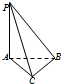 已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )
已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )| A、3π | ||||
| B、4π | ||||
C、
| ||||
| D、12π |
分析:取PC的中点O,连结OA、OB.由线面垂直的判定与性质,证出BC⊥PB且PA⊥AC,得到△PAC与△PBC是具有公共斜边的直角三角形,从而得出OA=OB=OC=OP=
PC,所以P、A、B、C四点在以O为球心的球面上.根据题中的数据,利用勾股定理算出PC长,进而得到球半径R=
,利用球的表面积公式加以计算,可得答案.
| 1 |
| 2 |
| ||
| 2 |
解答:解:取PC的中点O,连结OA、OB
 ∵PA⊥平面ABC,BC?平面ABC,∴PA⊥BC,
∵PA⊥平面ABC,BC?平面ABC,∴PA⊥BC,
又∵AC⊥BC,PA∩AC=A,∴BC⊥平面PAC,
∵PB?平面PAC,∴BC⊥PB,
∵OB是Rt△PBC的斜边上的中线,OB=
PC.
同理可得:Rt△PAC中,OA=
PC,
∴OA=OB=OC=OP=
PC,可得P、A、B、C四点在以O为球心的球面上.
Rt△ABC中,AC=BC=1,可得AC=
=
,
Rt△PAC中,PA=1,可得PC=
=
.
∴球O的半径R=
PC=
,可得球O的表面积为S=4πR2=4π×(
)2=3π.
故选:A
 ∵PA⊥平面ABC,BC?平面ABC,∴PA⊥BC,
∵PA⊥平面ABC,BC?平面ABC,∴PA⊥BC,又∵AC⊥BC,PA∩AC=A,∴BC⊥平面PAC,
∵PB?平面PAC,∴BC⊥PB,
∵OB是Rt△PBC的斜边上的中线,OB=
| 1 |
| 2 |
同理可得:Rt△PAC中,OA=
| 1 |
| 2 |
∴OA=OB=OC=OP=
| 1 |
| 2 |
Rt△ABC中,AC=BC=1,可得AC=
| AB2+BC2 |
| 2 |
Rt△PAC中,PA=1,可得PC=
| PA2+AC2 |
| 3 |
∴球O的半径R=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
故选:A
点评:本题给出特殊的三棱锥,由它的外接球的表面积.着重考查了线面垂直的判定与性质、勾股定理与球的表面积公式等知识,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
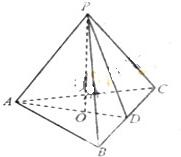 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.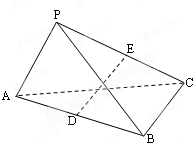 (2012•姜堰市模拟)如图,在三棱锥P-ABC中,已知AB=AC=2,PA=1,∠PAB=∠PAC=∠BAC=60°,点D、E分别为AB、PC的中点.
(2012•姜堰市模拟)如图,在三棱锥P-ABC中,已知AB=AC=2,PA=1,∠PAB=∠PAC=∠BAC=60°,点D、E分别为AB、PC的中点. (2013•广州二模)如图,在三棱锥P-ABC中,∠PAB=∠PAC=∠ACB=90°.
(2013•广州二模)如图,在三棱锥P-ABC中,∠PAB=∠PAC=∠ACB=90°.