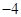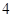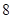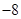题目内容
函数 零点的个数为( )
零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
C
解析试题分析:先求出函数的定义域,再把函数转化为对应的方程,在坐标系中画出两个函数y1=|x+1|,y2= 的图象求出方程的根的个数,即为函数
的图象求出方程的根的个数,即为函数 零点的个数.那么结合图像法
零点的个数.那么结合图像法
可知,由于它们公共点为(0,1),在y轴左侧必然有一个交点,在y轴上一个交点,而在y轴右侧,指数函数图像始终在直线的上方,因此可知必然有两个交点,从而说明函数的零点个数为2,选C.
考点:本题考查了函数零点、对应方程的根和函数图象之间的关系,通过转化和作图求出函数零点的个数,属于基础题。
点评:解决该试题的关键是对于当x=0时,它们有个公共点(0,1),这是问题的细节,也是一个易错点地方。注意特殊点的表示和应用。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设偶函数 满足
满足
 ,则
,则 ( )
( )
A. | B. |
C. | D. |
若方程 无实数解,则实数
无实数解,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 =
= 的定义域为( )
的定义域为( )
| A.[1,+∞) | B.[ ,1] ,1] | C.( ,+∞) ,+∞) | D.( ,1] ,1] |
定义域为 的函数
的函数
 有四个单调区间,则实数
有四个单调区间,则实数 满足( )
满足( )
A. | B. | C. | D. |
给定方程: ,下列命题中:(1) 该方程没有小于0的实数解;(2) 该方程有无数个实数解;(3) 该方程在(–∞,0)内有且只有一个实数解;
,下列命题中:(1) 该方程没有小于0的实数解;(2) 该方程有无数个实数解;(3) 该方程在(–∞,0)内有且只有一个实数解;
(4) 若x0是该方程的实数解,则x0>–1.
则正确命题的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,若实数
,若实数 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
定义在R上的偶函数 满足:对任意的
满足:对任意的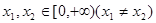 ,有
,有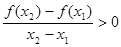 ,则( )
,则( )
A.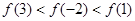 | B.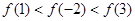 |
C.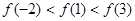 | D.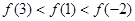 |
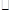 ”表示一种运算,即:
”表示一种运算,即: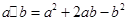 ,设函数
,设函数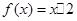 。且关于
。且关于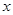 的方程为
的方程为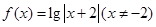 恰有四个互不相等的实数根
恰有四个互不相等的实数根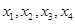 ,则
,则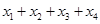 的值是( )
的值是( )