题目内容
定义域为 的函数
的函数
 有四个单调区间,则实数
有四个单调区间,则实数 满足( )
满足( )
A. | B. | C. | D. |
C
解析试题分析:函数 的图形是将
的图形是将 轴的右边翻折到左边得到的,所以图形要有4个单调区间,在
轴的右边翻折到左边得到的,所以图形要有4个单调区间,在 轴的右边必须有2个单调区间,即
轴的右边必须有2个单调区间,即 轴的右边的图形必须有一条对称轴,也就是
轴的右边的图形必须有一条对称轴,也就是 .
.
考点:本小题主要考查二次函数配方法研究其单调性,同时说明单调性与对称轴和开口方向有关.
点评:解决本小题关键是根据函数的对称性画出函数的图象,看是否满足题意.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
函数 的定义域为开区间(a,b),其导函数
的定义域为开区间(a,b),其导函数 在(a,b)内的图像如下图所示,则函数
在(a,b)内的图像如下图所示,则函数 在开区间(a,b)内极小值点的个数有( )
在开区间(a,b)内极小值点的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设函数 上单调递增,则
上单调递增,则 的大小关系为
的大小关系为
A.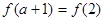 | B. |
C. | D.不确定 |
函数 零点的个数为( )
零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知函数 ,则
,则 ( )
( )
| A.-2 | B.10 | C.2 | D.-10 |
函数 在区间
在区间 内的零点个数是( )
内的零点个数是( )
| A.0 | B.1 | C.2 | D.3 |
 的图象大致是( )
的图象大致是( )
 的图像如左图所示,则函数
的图像如左图所示,则函数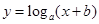 的图像可能是( )
的图像可能是( )
 为定义域,以
为定义域,以 为值域的函数是( )
为值域的函数是( )