题目内容
1.我校某高一学生为了获得华师一附中荣誉毕业证书,在“体音美2+1+1项目”中学习游泳.他每次游泳测试达标的概率都为60%,现采用随机模拟的方法估计该同学三次测试恰有两次达标的概率:先由计算器产生0到9之间的整数随机数,指定1,2,3,4表示未达标,5,6,7,8,9,0表示达标;再以每三个随机数为一组,代表三次测试的结果,经随机模拟产生了如下20组随机数:917 966 891 925 271 932 872 458 569 683
431 257 393 027 556 488 730 113 507 989
据此估计,该同学三次测试恰有两次达标的概率为( )
| A. | 0.50 | B. | 0.40 | C. | 0.43 | D. | 0.48 |
分析 由题意知模拟三次测试的结果,经随机模拟产生了如下20组随机数,在20组随机数中表示三次测试恰有两次达标的有可以通过列举得到共10组随机数,根据概率公式,得到结果.
解答 解:由题意知模拟三次测试的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三次测试恰有两次达标的有:917、891、925、872、458、683、027、257、488、507.
共10组随机数,
∴所求概率为$\frac{10}{20}$=0.5.
故选:A.
点评 本题考查模拟方法估计概率,是一个基础题,解这种题目的主要依据是等可能事件的概率,注意列举法在本题的应用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
11.${(2x-\frac{1}{x})^8}$的展开式中x2的系数为( )
| A. | -1792 | B. | 1792 | C. | -448 | D. | 448 |
12.$\int_{-2}^2{sinxdx=}$( )
| A. | -1 | B. | 1 | C. | 0 | D. | -8 |
9.若x,y∈R+且2x+y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值( )
| A. | $3+2\sqrt{2}$ | B. | $3-2\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
16.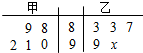 下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
 下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )
下面茎叶图表示的甲、乙两人在5次综合测评中的成绩,其中一个数字x被污损,则甲的平均成绩超过乙的平均成绩的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{4}{5}$ | D. | $\frac{9}{10}$ |
 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为45°,则此山的高度CD=300$\sqrt{2}$m.
如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为45°,则此山的高度CD=300$\sqrt{2}$m.