题目内容
已知圆C与两坐标轴都相切,圆心C到直线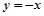 的距离等于
的距离等于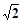 .
.
(1)求圆C的方程.
(2)若直线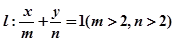 与圆C相切,求证:
与圆C相切,求证: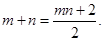
【答案】
(1) .
(2)
.
(2) 
【解析】
试题分析:(1)设圆C半径为 ,由已知得:
,由已知得:
∴ ,或
,或
∴圆C方程为 .
.
(2)直线 ,∵
,∵
∴
∴
左边展开,整理得,
∴
考点:本题主要考查圆的方程,直线与圆的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求圆的方程时,主要运用了圆的特征三角形—半径、弦长的一半、圆心到直线的距离三者关系。(II)小题中,点到直线的距离等于半径,确定得到m,n的关系。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
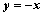 的距离等于
的距离等于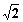 .
.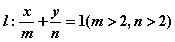 与圆C相切,求
与圆C相切,求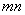 的最小值.
的最小值.