题目内容
已知圆C与两坐标轴都相切,圆心C到直线y=-x的距离等于| 2 |
(1)求圆C的方程.
(2)若直线l:
| x |
| m |
| y |
| n |
| 2 |
分析:(1)由已知得:
,求出a,b,r 的值,即得圆C方程.
(2)根据直线和圆相切可得
=1,化简可得m+n=
,再由基本不等式可得(
)2-4
+2≥0,解得
≥2+
,从而得到mn≥6+4
.
|
(2)根据直线和圆相切可得
| |n+m-mn| | ||
|
| mn+2 |
| 2 |
| mn |
| mn |
| mn |
| 2 |
| 2 |
解答:解:(1)设圆C半径为r,由已知得:
,∴
,或
,
∴圆C方程为(x-1)2+(y-1)2=1,或(x+1)2+(y+1)2=1.
(2)直线l方程为nx+my-mn=0,∵直线l与圆C:(x-1)2+(y-1)2=1相切,∴
=1,
∴(n+m-mn)2=n2+m2,左边展开,整理得,mn=2m+2n-2.∴m+n=
.
∵m>0,n>0,m+n≥2
,∴
≥2
,∴(
)2-4
+2≥0,
∴
≥2+
,或
≤2-
.∵m>2,n>2,∴
≥2+
,
∴mn≥6+4
.
|
|
|
∴圆C方程为(x-1)2+(y-1)2=1,或(x+1)2+(y+1)2=1.
(2)直线l方程为nx+my-mn=0,∵直线l与圆C:(x-1)2+(y-1)2=1相切,∴
| |n+m-mn| | ||
|
∴(n+m-mn)2=n2+m2,左边展开,整理得,mn=2m+2n-2.∴m+n=
| mn+2 |
| 2 |
∵m>0,n>0,m+n≥2
| mn |
| mn+2 |
| 2 |
| mn |
| mn |
| mn |
∴
| mn |
| 2 |
| mn |
| 2 |
| mn |
| 2 |
∴mn≥6+4
| 2 |
点评:本题考查圆的标准方程,直线和圆的位置关系,点到直线的距离公式,基本不等式的应用,得到m+n=
是解题的
关键.
| mn+2 |
| 2 |
关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
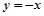 的距离等于
的距离等于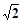 .
.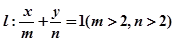 与圆C相切,求证:
与圆C相切,求证: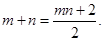
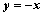 的距离等于
的距离等于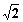 .
.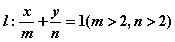 与圆C相切,求
与圆C相切,求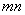 的最小值.
的最小值.