题目内容
 将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点O为中心﹐其中
将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点O为中心﹐其中| x |
| y |
| x |
| y |
| A、2 | B、3 | C、4 | D、5 |
考点:平面向量坐标表示的应用,平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据题意,画出图形,结合图形,得出求a+b的最大值时﹐只需考虑图中6个顶点的向量即可,分别求出即得结论.
解答:
解:因为想求a+b的最大值﹐所以考虑图中的6个顶点的向量即可;讨论如下﹕
(1)因为
=
﹐所以(a,b)=(1,0);
(2)因为
=
+
=
+3
=3
+
﹐所以(a,b)=(3,1);
(3)因为
=
+
=
+2
=2
+
﹐所以(a,b)=(2,1);
(4)因为
=
+
+
=
+
+
=
+
+(
+2
)=3
+2
﹐
所以(a,b)=(3,2);
(5)因为
=
+
=
+
=
+
﹐所以(a,b)=(1,1);
(6)因为
=
﹐所以(a,b)=(0,1);
因此﹐a+b的最大值为3+2=5﹒
故选:D﹒
(1)因为
| OA |
| x |
(2)因为
| OB |
| OF |
| FB |
| y |
| x |
| x |
| y |
(3)因为
| OC |
| OF |
| FC |
| y |
| x |
| x |
| y |
(4)因为
| OD |
| OF |
| FE |
| ED |
| y |
| x |
| OC |
| y |
| x |
| y |
| x |
| x |
| y |
所以(a,b)=(3,2);
(5)因为
| OE |
| OF |
| FE |
| y |
| x |
| x |
| y |
(6)因为
| OF |
| y |
因此﹐a+b的最大值为3+2=5﹒
故选:D﹒
点评:本题考查了平面向量的基本定理的应用问题,也考查了平面向量的坐标表示的应用问题,是基础题目.

练习册系列答案
相关题目
设二次函数f(x)=ax2+bx+c的导函数为f′(x),对?x∈R,不等式f(x)≥f′(x)恒成立,则
的最大值为( )
| b2 |
| a2+2c2 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
下列说法正确的是( )
| A、一个平面的面积可以是16cm2 |
| B、空间三点可以确定一个平面 |
| C、平面α与平面β相交于线段AB |
| D、两条相交直线可以确定一个平面 |
直线x+y=1和圆:x2+y2-6x+8y-24=0的位置关系是( )
| A、相切 | B、相交 | C、相离 | D、不确定 |
一个长方体,其正视图面积为
,侧视图面积为
,俯视图面积为
,则长方体的外接球的表面积为( )
| 6 |
| 3 |
| 2 |
| A、6π | ||
| B、24π | ||
C、6
| ||
D、
|
一个正八面体的八个顶点都在同一个球面上,如果该正八面体的棱长为
.则这个球的表面积为( )
| 2 |
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
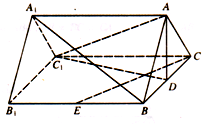 如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.