题目内容
直线l:3x+4y-12=0与椭圆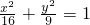 相交于A、B两点,点P是椭圆上的一点,若三角形PAB的面积为12,则满足条件的点P的个数为
相交于A、B两点,点P是椭圆上的一点,若三角形PAB的面积为12,则满足条件的点P的个数为
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:由题意可得AB=5,则由三角形PAB的面积为12可得AB的距离 h= ,作与AB平行的直线l,使l与椭圆
,作与AB平行的直线l,使l与椭圆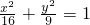 相切,设直线l的方程为
相切,设直线l的方程为  ,把l的方程代入椭圆方程化简,由判别式等于0 解得 k值,从而得到直线l的方程,求出直线l与AB间的距离,将此距离和h作比较,从而得出结论.
,把l的方程代入椭圆方程化简,由判别式等于0 解得 k值,从而得到直线l的方程,求出直线l与AB间的距离,将此距离和h作比较,从而得出结论.
解答:由已知可得A(4,0),B(0,3),AB=5,由12= AB•h,可得P到AB的距离 h=
AB•h,可得P到AB的距离 h= .
.
作与AB平行的直线l,使l与椭圆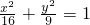 相切,设直线l的方程为
相切,设直线l的方程为  ,
,
把l的方程代入椭圆方程化简可得 x2-4kx+8k2-8=0,
由△=16k2-32(k2-1)=0
∴k= ,或 k=-
,或 k=- ,
,
故直线l的方程为 ,或
,或  .
.
因为 与AB的距离为
与AB的距离为  =
= <
< ,
,
 与AB的距离为
与AB的距离为  =
= >
> .故这样的点P共有 2个,
.故这样的点P共有 2个,
故选 B.
点评:本题考查直线和圆锥曲线的位置关系,两平行线间的距离公式,得到与AB平行的且与椭圆相切的切线l 的方程的个数是解题的关键.
分析:由题意可得AB=5,则由三角形PAB的面积为12可得AB的距离 h=
 ,作与AB平行的直线l,使l与椭圆
,作与AB平行的直线l,使l与椭圆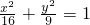 相切,设直线l的方程为
相切,设直线l的方程为  ,把l的方程代入椭圆方程化简,由判别式等于0 解得 k值,从而得到直线l的方程,求出直线l与AB间的距离,将此距离和h作比较,从而得出结论.
,把l的方程代入椭圆方程化简,由判别式等于0 解得 k值,从而得到直线l的方程,求出直线l与AB间的距离,将此距离和h作比较,从而得出结论.解答:由已知可得A(4,0),B(0,3),AB=5,由12=
 AB•h,可得P到AB的距离 h=
AB•h,可得P到AB的距离 h= .
.作与AB平行的直线l,使l与椭圆
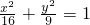 相切,设直线l的方程为
相切,设直线l的方程为  ,
,把l的方程代入椭圆方程化简可得 x2-4kx+8k2-8=0,
由△=16k2-32(k2-1)=0
∴k=
 ,或 k=-
,或 k=- ,
,故直线l的方程为
 ,或
,或  .
.因为
 与AB的距离为
与AB的距离为  =
= <
< ,
, 与AB的距离为
与AB的距离为  =
= >
> .故这样的点P共有 2个,
.故这样的点P共有 2个,故选 B.
点评:本题考查直线和圆锥曲线的位置关系,两平行线间的距离公式,得到与AB平行的且与椭圆相切的切线l 的方程的个数是解题的关键.

练习册系列答案
相关题目
 (2012•江苏二模)选做题
(2012•江苏二模)选做题