题目内容
4.已知函数f(x)=ax3+bx-2,a,b∈R,若f(-2)=-1,则f(2)的值为-3.分析 根据条件建立方程关系进行求解即可.
解答 解:∵f(-2)=-1,
∴-8a-2b-2=-1,即8a+2b=-1,
则f(2)=8a+2b-2=-2-1=-3,
故答案为:-3.
点评 本题主要考查函数值的计算,根据条件建立方程是解决本题的关键.

练习册系列答案
相关题目
14.如图所给的程序运行结果为S=41,那么判断框中应填入的关于k的条件是( )


| A. | k≥6 | B. | k≥5 | C. | k>6 | D. | k>5 |
19.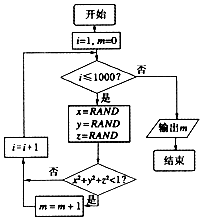 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )
 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( )| A. | 3.119 | B. | 3.126 | C. | 3.132 | D. | 3.151 |
9.已知集合A={x|x2-2x-3>0},集合B={x∈Z|x2≤4x},则∁RA∩B=( )
| A. | {x|0≤x≤3} | B. | {-1,0,1,2,3} | C. | {0,1,2,3} | D. | {1,2} |
16.命题“?x∈[1,3],x2≤a”为真命题的一个充分不必要条件是( )
| A. | a≤9 | B. | a≥9 | C. | a≤10 | D. | a≥10 |