题目内容
设函数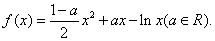
(Ⅰ)当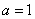 时,求函数
时,求函数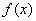 的极值;
的极值;
(Ⅱ)当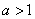 时,讨论函数
时,讨论函数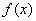 的单调性.
的单调性.
(Ⅲ)若对任意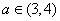 及任意
及任意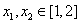 ,恒有
,恒有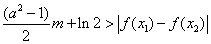 成立,求实数
成立,求实数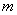 的取值范围.
的取值范围.
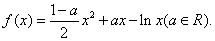
(Ⅰ)当
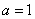 时,求函数
时,求函数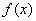 的极值;
的极值;(Ⅱ)当
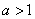 时,讨论函数
时,讨论函数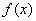 的单调性.
的单调性.(Ⅲ)若对任意
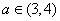 及任意
及任意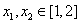 ,恒有
,恒有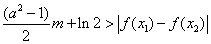 成立,求实数
成立,求实数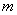 的取值范围.
的取值范围.(1)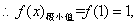 无极大值.
无极大值.
(2)当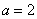 时,
时,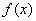 在
在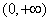 上是减函数;
上是减函数;
当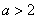 时,
时,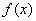 在
在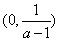 和
和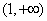 单调递减,在
单调递减,在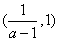 上单调递增;
上单调递增;
当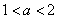 时,
时,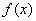 在
在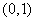 和
和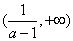 单调递减,在
单调递减,在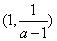 上单调递增;
上单调递增;
(3)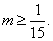
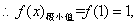 无极大值.
无极大值.(2)当
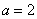 时,
时,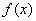 在
在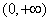 上是减函数;
上是减函数;当
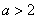 时,
时,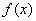 在
在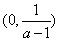 和
和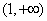 单调递减,在
单调递减,在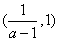 上单调递增;
上单调递增;当
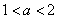 时,
时,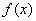 在
在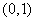 和
和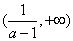 单调递减,在
单调递减,在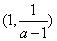 上单调递增;
上单调递增; (3)
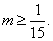
试题分析:解:(Ⅰ)函数的定义域为
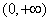 .(2分)
.(2分)当
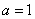 时,
时,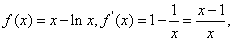 (4分)
(4分)当
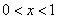 时,
时,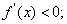 当
当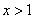 时,
时,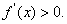
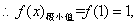 无极大值.(6分)
无极大值.(6分)(Ⅱ)
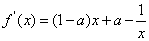
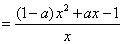
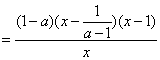 (7分)
(7分)当
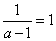 ,即
,即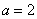 时,
时,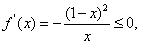
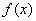 在定义域上是减函数;
在定义域上是减函数;当
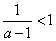 ,即
,即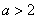 时,令
时,令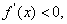 得
得 或
或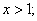
令
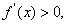 得
得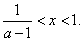
当
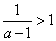 ,即
,即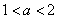 时,令
时,令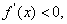 得
得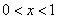 或
或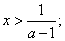
令
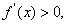 得
得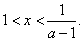
综上,当
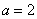 时,
时,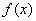 在
在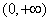 上是减函数;
上是减函数;当
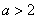 时,
时,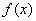 在
在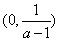 和
和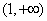 单调递减,在
单调递减,在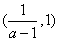 上单调递增;
上单调递增;当
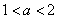 时,
时,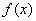 在
在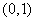 和
和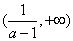 单调递减,在
单调递减,在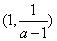 上单调递增;
上单调递增; (10分)
(Ⅲ)由(Ⅱ)知,当
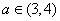 时,
时,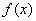 在
在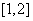 上单减,
上单减,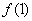 是最大值,
是最大值,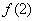 是最小值.
是最小值.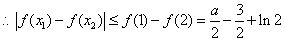 , (12分)
, (12分)
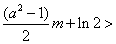
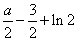 ,而
,而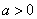 经整理得
经整理得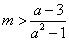 ,
,由
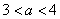 得
得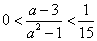 ,所以
,所以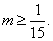 (15分)
(15分)点评:主要是考查了导数在研究函数中的运用,利用导数判定单调性以及极值和最值,属于中档题。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 (安)随时间
(安)随时间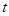 (秒)变化的函数
(秒)变化的函数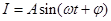
 的
的 时,电流强度是( )
时,电流强度是( )
 安
安 安
安 安
安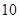 安
安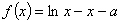 有两个不同的零点,则实数
有两个不同的零点,则实数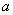 的取值范围是
的取值范围是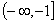
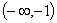
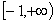

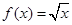 ,
,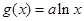 ,
,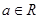
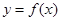 与曲线
与曲线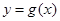 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求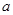 的值及该切线的方程;
的值及该切线的方程;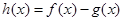 ,当
,当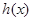 存在最小值时,求其最小值
存在最小值时,求其最小值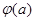 的解析式;
的解析式;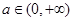 时,
时, 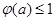 .
.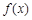 是定义在
是定义在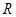 上的偶函数,且对任意
上的偶函数,且对任意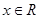 ,都有
,都有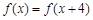 ,当
,当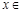
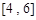 时,
时,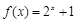 ,则函数
,则函数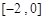 上的反函数
上的反函数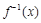 的值
的值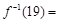 ( )
( )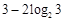



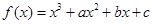 在
在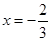 与
与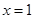 时都取得极值
时都取得极值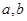 的值与函数
的值与函数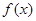 的单调区间
的单调区间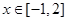 ,不等式
,不等式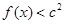 恒成立,求
恒成立,求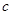 的取值范围。
的取值范围。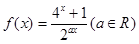 是偶函数,
是偶函数,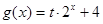 ,
,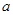 的值;(2)当
的值;(2)当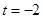 时,求
时,求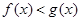 的解集;
的解集;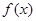 的图象总在
的图象总在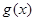 的图象上方,求实数
的图象上方,求实数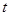 的取值范围.
的取值范围.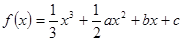 在
在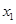 处取得极大值,在
处取得极大值,在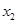 处取得极小值,满足
处取得极小值,满足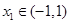 ,
,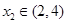 ,则
,则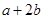 的取值范围是
的取值范围是