题目内容
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(1)证明AB⊥平面VAD;
(2)求面VAD与面VDB所成的二面角的大小.

证明:(1)作AD的中点O,则VO⊥底面ABCD.
建立如图空间直角坐标系,并设正方形边长为1,

则A(![]() ,0,0),B(
,0,0),B(![]() ,1,0),C(
,1,0),C(![]() ,1,0),D(
,1,0),D(![]() ,0,0),V(0,0,
,0,0),V(0,0,![]() ),
),
∴![]() =(0,1,0),
=(0,1,0),![]() =(-1,0,0),
=(-1,0,0),![]() =(
=(![]() ,0,
,0,![]() ).
).
由![]() ·
·![]() =(0,1,0)·(-1,0,0)=0
=(0,1,0)·(-1,0,0)=0![]()
![]() ⊥
⊥![]() ,
,
![]() ·
·![]() =(0,1,0)·(
=(0,1,0)·(![]() ,0,
,0,![]() )=0
)=0![]()
![]() ⊥
⊥![]() .
.
又AB∩AV=A,∴AB⊥平面VAD.
(2)由(1)得![]() =(0,1,0)是面VAD的法向量.
=(0,1,0)是面VAD的法向量.
设n=(1,y,z)是面VDB的法向量,则

![]()

![]()

![]() n=(1,-1,
n=(1,-1,![]() ).
).
∴cos〈![]() ,n〉
,n〉![]() .
.
∴面VAD与面VDB所成的二面角的大小为π-arccos![]() .
.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
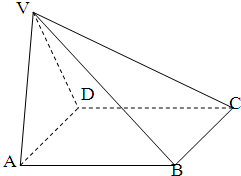 如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD
如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD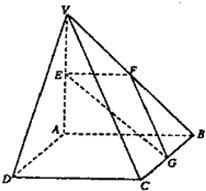 如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.
如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.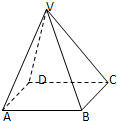 如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为
如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.