题目内容
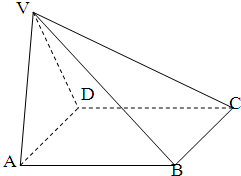如图，在四棱锥V-ABCD中底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD（1）证明：AB⊥平面VAD；
（2）求面VAD与面VDB所成的二面角的余弦值．
分析：（1）由已知中平面VAD⊥底面ABCD，ABCD是正方形，我们根据正方形的性质及面面垂直的性质定理，得到AB⊥平面VAD；
（2）取VD中点E，连接AE，BE，可得∠AEB即为所求的二面角的平面角，解△AEB即可得到面VAD与面VDB所成的二面角的余弦值；
（2）取VD中点E，连接AE，BE，可得∠AEB即为所求的二面角的平面角，解△AEB即可得到面VAD与面VDB所成的二面角的余弦值；
解答：证明：（1）平面VAD⊥平面ABCD，AB⊥AD，AB?平面ABCD，
平面VAD∩平面ABCD=AD，∴AB⊥面VAD
（2）取VD中点E，连接AE，BE，∵△VAD是正三角形，∴AE⊥VD，AE=
AD
∵AB⊥面VAD，AE，VD?平面VAD
∴AB⊥VD，AB⊥AE∴AE⊥VD，AB⊥VD，AB∩AE=A，且AB，AE?平面ABE，D
VD⊥平面ABE，∵BE?平面ABE，∴BE⊥VD，
∴∠AEB即为所求的二面角的平面角．
在RT△ABE中，tan∠AEB=
=
，
cos∠AEB=
平面VAD∩平面ABCD=AD，∴AB⊥面VAD
（2）取VD中点E，连接AE，BE，∵△VAD是正三角形，∴AE⊥VD，AE=
| ||
| 2 |
∵AB⊥面VAD，AE，VD?平面VAD
∴AB⊥VD，AB⊥AE∴AE⊥VD，AB⊥VD，AB∩AE=A，且AB，AE?平面ABE，D
VD⊥平面ABE，∵BE?平面ABE，∴BE⊥VD，
∴∠AEB即为所求的二面角的平面角．
在RT△ABE中，tan∠AEB=
| AB |
| AE |
| 2 |
| 3 |
| 3 |
cos∠AEB=
| ||
| 7 |
点评：本题考查的知识点是直线与平面垂直的判定，二面角的平面角及求法，（1）的关键是熟练掌握面面垂直的性质定理，（2）的关键是找到二面角的平面角，将二面角问题转化为解三角形问题．
练习册系列答案
相关题目
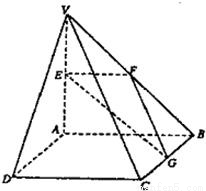
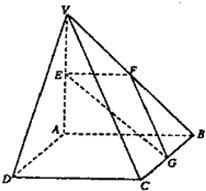如图，在四棱锥V-ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点．
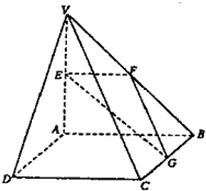如图，在四棱锥V-ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点．
