题目内容
已知两个单位向量
，
的夹角为120°，向量t
+（1-t）
与
垂直，则t= ．
| a |
| b |
| a |
| b |
| a |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据两非零向量垂直的充要条件及已知条件即可得到：[t
+（1-t）
]•
=0，进行数量积的运算即可求出t．
| a |
| b |
| a |
解答：
解：由已知条件知：[t
+(1-t)
]•
=t
2+(1-t)
•
=t+
=
=0；
∴t=
．
故答案为：
．
| a |
| b |
| a |
| a |
| b |
| a |
| t-1 |
| 2 |
| 3t-1 |
| 2 |
∴t=
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：考查两非零向量垂直的充要条件，单位向量，向量数量积的运算．
练习册系列答案
名校课堂系列答案
相关题目
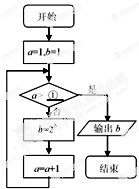已知流程图如图（a=1，b=1下分别是a＞①，b=2b，a=+1）所示，该程序运行后，为使输出的b值为16，则循环体的判断框内①处应填的是（ ）