题目内容
(本小题满分14分)已知函数 .
.
(1)求 的定义域;
的定义域;
(2)在函数 的图像上是否存在不同的两点,使过此两点的直线平行于
的图像上是否存在不同的两点,使过此两点的直线平行于 轴;
轴;
(3)当 满足什么关系时,
满足什么关系时, 在
在 上恒取正值.
上恒取正值.
(1)(0,+∞);(2)不存在;(3)
【解析】
试题分析:(1)由ax-bx>0得 ,由已知
,由已知 ,故x>0,
,故x>0,
即f(x)的定义域为(0,+∞)
(2)任取 ,∵a>1>b>0
,∵a>1>b>0
∴ ,则
,则 ,
,
故 ,
,
∴ ,即
,即
∴f(x)在(0,+∞)上为增函数.
假设函数y=f(x)的图像上存在不同的两点 ,使直线AB平行于x轴,即
,使直线AB平行于x轴,即 ,
,
这与f(x)是增函数矛盾.故函数y=f(x)的图像上不存在不同的两点,使过这两点的直线平行于x轴.
(3)由(2)知,f(x)在 是增函数,
是增函数,
∴f(x)在 上也是增函数
上也是增函数
∴当 时,
时, .
.
∴只需 ,即
,即 lg
lg ,即
,即 ,
,
 时,f(x)在
时,f(x)在 上恒取正值.
上恒取正值.
考点:本题考查对数函数的单调性与特殊点;对数函数的定义域.

练习册系列答案
相关题目
 在区间
在区间 内可导,且
内可导,且 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 的图象是
的图象是
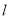 的对称点为B(7,-4),则直线
的对称点为B(7,-4),则直线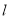 的方程是________.
的方程是________. ,求函数
,求函数 的最大值和最小值.
的最大值和最小值. B.
B. C.
C. D.
D.
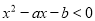 的解集为{x|2<x<3},则a+b=________.
的解集为{x|2<x<3},则a+b=________. 的离心率e=
的离心率e= ,A,B是椭圆的左右顶点,P为椭圆上不同于AB的动点,直线PA,PB的倾斜角分别为
,A,B是椭圆的左右顶点,P为椭圆上不同于AB的动点,直线PA,PB的倾斜角分别为 ,则
,则 = .
= .