题目内容
10.在平面直角坐标系xOy中,设A、B、C是圆x2+y2=1上相异三点.若存在正实数λ,μ,使得$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,则(λ-2)2+μ2的取值范围是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,2) | C. | (2,+∞) | D. | (-∞,$\frac{1}{2}$) |
分析 由条件可以得到$-1<\overrightarrow{OA}•\overrightarrow{OC}<1$,而根据$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$便可得到${μ}^{2}=1+{λ}^{2}-2λ\overrightarrow{OA}•\overrightarrow{OC}$,这样带入$(λ-2)^{2}+{μ}^{2}=(λ-2)^{2}+1+{λ}^{2}-2λ\overrightarrow{OA}•\overrightarrow{OC}$,根据$-1<\overrightarrow{OA}•\overrightarrow{OC}<1$便可得到2λ2-6λ+5<(λ-2)2+μ2<2λ2-2λ+5,根据二次函数的值域便可得出(λ-2)2+μ2的取值范围.
解答 解:根据题意,$-1<\overrightarrow{OA}•\overrightarrow{OC}<1$;
由$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$得,$μ\overrightarrow{OB}=\overrightarrow{OC}-λ\overrightarrow{OA}$;
∴${μ}^{2}=1+{λ}^{2}-2λ\overrightarrow{OA}•\overrightarrow{OC}$;
∴(λ-2)2+μ2=(λ-2)2+1+λ2$-2λ\overrightarrow{OA}•\overrightarrow{OC}$;
∵λ>0;
∴(λ-2)2+1+λ2-2λ<$(λ-2)^{2}+1+{λ}^{2}-2λ\overrightarrow{OA}•\overrightarrow{OC}$<(λ-2)2+1+λ2+2λ;
(λ-2)2+1+λ2-2λ=2λ2-6λ+5$>\frac{1}{2}$;
(λ-2)2+1+λ2+2λ=2λ2-2λ+5无最大值;
∴(λ-2)2+μ2的取值范围为$(\frac{1}{2},+∞)$.
故选A.
点评 考查向量数乘的几何意义,向量数量积的计算公式,以及不等式的性质,二次函数的值域.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | ($\frac{1}{x}$)′=$\frac{1}{{x}^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | C. | (3x+1)′=x•3x-1+1 | D. | (cosx)′=sinx |
| A. | 7,11,18 | B. | 6、12、18 | C. | 6、13、17 | D. | 7、14、21 |
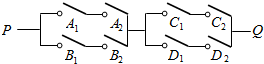 如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.
如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.| A.49 | B.56 | C.200 | D.207 | E.360 | F.269. |
 的定义域,值域分别是
的定义域,值域分别是 、
、 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.