题目内容
一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为p,出现“×”的概率为q.若第k次出现“○”,则ak=1;出现“×”,则ak=-1.令Sn=a1+a2+…+an(n∈N*).(1)当p=q=
 时,求S6≠2的概率;
时,求S6≠2的概率;(2)当p=
 ,q=
,q= 时,求S8=2且Si≥0(i=1,2,3,4)的概率.
时,求S8=2且Si≥0(i=1,2,3,4)的概率.
【答案】分析:(1)先求S6=2的概率,则在6次变化中,出现“○”有4次,出现“×”有2次.求出S6=2的概率,再用1减去此概率,即可求得S6≠2的概率.
(2)当S8=2时,即前八秒出现“○”5次和“×”3次,又已知Si≥0(i=1,2,3,4),若第一、三秒出现“○”,则其余六秒可任意出现“○”3次;若第一、二秒出现“○”,第三秒出现“×”,则后五秒可任出现“○”3次.由此求得S8=2的概率为P=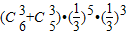 ,运算求得结果.
,运算求得结果.
解答:解:(1)当p=q= 时,先求S6=2的概率,则在6次变化中,出现“○”有4次,出现“×”有2次.
时,先求S6=2的概率,则在6次变化中,出现“○”有4次,出现“×”有2次.
故S6=2的概率为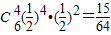 .
.
∴S6≠2的概率为P1=1-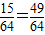 .
.
(2)当S8=2时,即前八秒出现“○”5次和“×”3次,又已知Si≥0(i=1,2,3,4),
若第一、三秒出现“○”,则其余六秒可任意出现“○”3次;
若第一、二秒出现“○”,第三秒出现“×”,则后五秒可任出现“○”3次.
故此时的概率为P=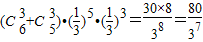 =
=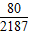 .
.
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,体现了转化的数学思想,属于中档题.
(2)当S8=2时,即前八秒出现“○”5次和“×”3次,又已知Si≥0(i=1,2,3,4),若第一、三秒出现“○”,则其余六秒可任意出现“○”3次;若第一、二秒出现“○”,第三秒出现“×”,则后五秒可任出现“○”3次.由此求得S8=2的概率为P=
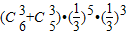 ,运算求得结果.
,运算求得结果.解答:解:(1)当p=q=
 时,先求S6=2的概率,则在6次变化中,出现“○”有4次,出现“×”有2次.
时,先求S6=2的概率,则在6次变化中,出现“○”有4次,出现“×”有2次.故S6=2的概率为
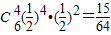 .
.∴S6≠2的概率为P1=1-
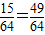 .
.(2)当S8=2时,即前八秒出现“○”5次和“×”3次,又已知Si≥0(i=1,2,3,4),
若第一、三秒出现“○”,则其余六秒可任意出现“○”3次;
若第一、二秒出现“○”,第三秒出现“×”,则后五秒可任出现“○”3次.
故此时的概率为P=
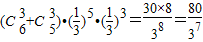 =
=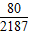 .
.点评:本题主要考查n次独立重复实验中恰好发生k次的概率,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目