题目内容
12.设m、n∈R,且5m+12n=13,则m2+n2的最小值为( )| A. | $\frac{1}{169}$ | B. | $\frac{1}{13}$ | C. | 1 | D. | 13 |
分析 由题意知所求点(m,n)为直线上到原点距离最小值的平方,由此能求出m2+n2的最小值.
解答 解:由题意知m2+n2的最小值表示点(m,n)为直线上到原点最近的点,
由原点到直线的距离为$\frac{|13|}{\sqrt{{5}^{2}+1{2}^{2}}}$=1,
∴m2+n2的最小值为1;
.故选:C
点评 本题考查点到直线的距离的最小值,解题时要认真审题,仔细解答,注意合理地进行等价转化.也可以利用二次函数的最值求解.

练习册系列答案
相关题目
7.函数f(x)=2cos(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则f(0)的值( )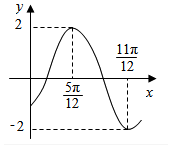

| A. | $-\frac{3}{2}$ | B. | -1 | C. | $-\sqrt{2}$ | D. | $-\sqrt{3}$ |
17.执行如图所示的程序框图,则输出的S等于( )
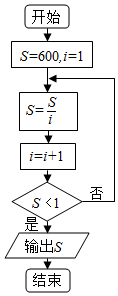

| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
1.已知F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1且垂直于实轴的直线与双曲线的两条渐近线分别相交于A、B两点,若坐标原点O恰为△ABF2的垂心(三角形三条高的交点),则双曲线的离心率为( )
| A. | $\frac{\sqrt{21}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
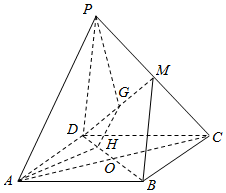 如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.
如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H. 已知抛物线y2=2px的焦点F(1,0),过F作直线l交抛物线于A(x1,y1),B(x2,y2)两点,如图所示,A在x轴上方.
已知抛物线y2=2px的焦点F(1,0),过F作直线l交抛物线于A(x1,y1),B(x2,y2)两点,如图所示,A在x轴上方.