题目内容
把函数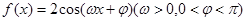 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移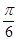 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2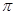 的奇函数
的奇函数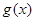 .
.
(1) 求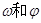 的值;
的值;
(2)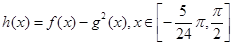 的单调区间和最值.
的单调区间和最值.
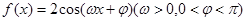 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移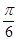 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2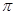 的奇函数
的奇函数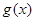 .
.(1) 求
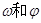 的值;
的值;(2)
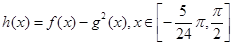 的单调区间和最值.
的单调区间和最值.(1)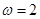
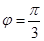
(2)递增区间为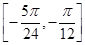 、
、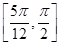 , 递减区间为
, 递减区间为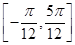
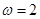
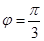
(2)递增区间为
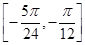 、
、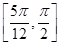 , 递减区间为
, 递减区间为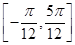
(1)根据函数图像的伸缩和平移变换规律得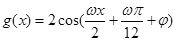 ,又奇函数
,又奇函数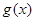 的一个最小正周期为2
的一个最小正周期为2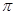 ,所以
,所以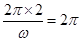 得
得 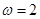 ,
, ,
,
所以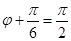 ,即
,即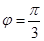 ;(2)结合(1)得
;(2)结合(1)得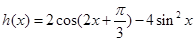 利用两角和的余弦公式和二倍角的余弦公式化简
利用两角和的余弦公式和二倍角的余弦公式化简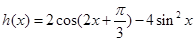 为一个角的三角函数的形式即
为一个角的三角函数的形式即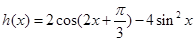
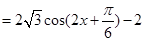 .因为
.因为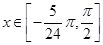 ,所以
,所以 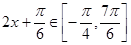 ,根据余弦函数的单调性和最值可得
,根据余弦函数的单调性和最值可得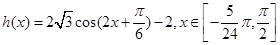 的单调区间和最值.
的单调区间和最值.
(1)图象变化后得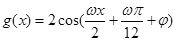
由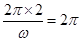 得
得 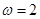 则
则 ………………6
………………6
又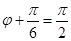 所以
所以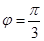
(2)由(1)得
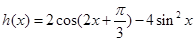
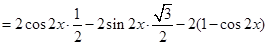
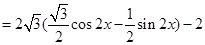
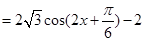 …………………10
…………………10
∵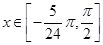 ∴
∴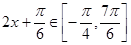
∴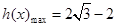
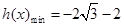
递增区间为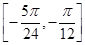 、
、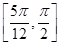 ,
,
递减区间为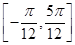
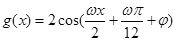 ,又奇函数
,又奇函数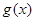 的一个最小正周期为2
的一个最小正周期为2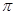 ,所以
,所以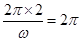 得
得 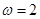 ,
, ,
,所以
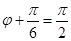 ,即
,即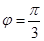 ;(2)结合(1)得
;(2)结合(1)得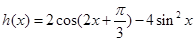 利用两角和的余弦公式和二倍角的余弦公式化简
利用两角和的余弦公式和二倍角的余弦公式化简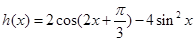 为一个角的三角函数的形式即
为一个角的三角函数的形式即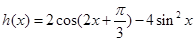
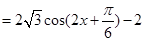 .因为
.因为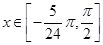 ,所以
,所以 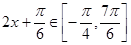 ,根据余弦函数的单调性和最值可得
,根据余弦函数的单调性和最值可得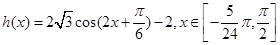 的单调区间和最值.
的单调区间和最值.(1)图象变化后得
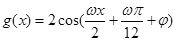
由
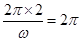 得
得 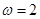 则
则 ………………6
………………6又
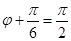 所以
所以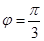
(2)由(1)得
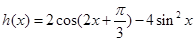
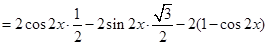
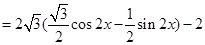
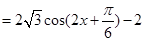 …………………10
…………………10∵
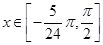 ∴
∴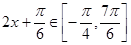
∴
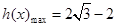
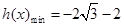
递增区间为
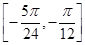 、
、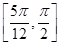 ,
, 递减区间为
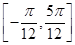

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
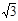 sinx)-1, x∈R.
sinx)-1, x∈R. 中,
中,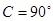 ,求f (A)的取值范围.
,求f (A)的取值范围.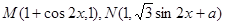
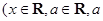 是常数),且
是常数),且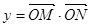 (其中
(其中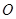 为坐标原点).
为坐标原点).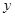 关于
关于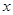 的函数关系式
的函数关系式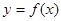 ;
;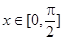 时,
时,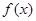 的最大值为4,求
的最大值为4,求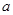 的值.
的值.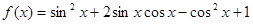
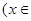 R
R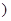 .
.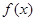 的最大值,并指出此时
的最大值,并指出此时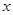 的值.
的值. 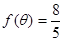 ,求
,求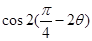 的值.
的值.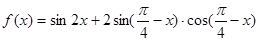
 的最小正周期; (2) 求函数
的最小正周期; (2) 求函数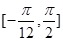 上的值域;
上的值域;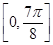 上的简图,并且依图写出函数
上的简图,并且依图写出函数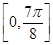 上的递增区间.
上的递增区间.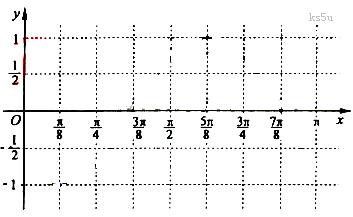
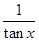 )sin2x-2sin(x+
)sin2x-2sin(x+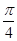 )sin(x-
)sin(x- ,
,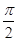 ],求f(x)的取值范围
],求f(x)的取值范围 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、b、c,若
、b、c,若 ,
, ,且
,且 .
. ,三角形面积
,三角形面积 ,求
,求 的值
的值 ,求2b+c的取值范围.
,求2b+c的取值范围.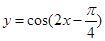 的图象,只需将函数
的图象,只需将函数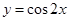 的图象( )
的图象( ) 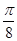 个单位
个单位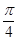 个单位
个单位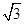 cosωx
cosωx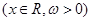 满足f(α)=-2,f(β)=0,且|α-β|的最小值为
满足f(α)=-2,f(β)=0,且|α-β|的最小值为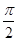 ,则函数f(x)的单调增区间为_____________
,则函数f(x)的单调增区间为_____________