题目内容
已知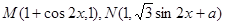
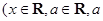 是常数),且
是常数),且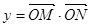 (其中
(其中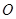 为坐标原点).
为坐标原点).
(1)求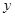 关于
关于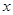 的函数关系式
的函数关系式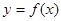 ;
;
(2)求函数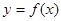 的单调区间;
的单调区间;
(3)若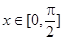 时,
时,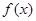 的最大值为4,求
的最大值为4,求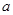 的值.
的值.
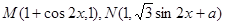
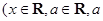 是常数),且
是常数),且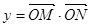 (其中
(其中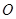 为坐标原点).
为坐标原点).(1)求
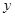 关于
关于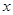 的函数关系式
的函数关系式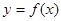 ;
;(2)求函数
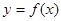 的单调区间;
的单调区间;(3)若
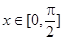 时,
时,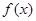 的最大值为4,求
的最大值为4,求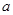 的值.
的值.(1)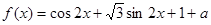 .(2)增区间为
.(2)增区间为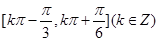 ,
,
单调递减区间为 .(3)
.(3)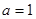 .
.
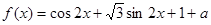 .(2)增区间为
.(2)增区间为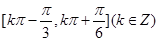 ,
,单调递减区间为
 .(3)
.(3)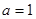 .
.(1)数量积的坐标运算;(2)利用辅助角公式化简函数,由复合函数的单调性,解不等式;
(3)先确定得到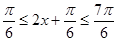 ,将
,将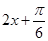 看作t,研究函数y=sint在
看作t,研究函数y=sint在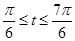 的最值情况。
的最值情况。
解:(1)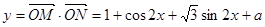 ,
,
所以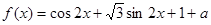 .
.
(2)由(1)可得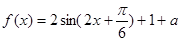 ,
,
由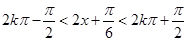 , 解得
, 解得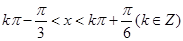 ;
;
由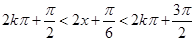 , 解得
, 解得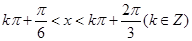 ,
,
所以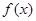 的单调递增区间为
的单调递增区间为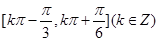 ,
,
单调递减区间为 .
.
(3)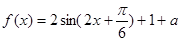 ,因为
,因为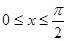 , 所以
, 所以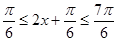 ,
,
当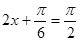 ,即
,即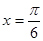 时,
时,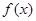 取最大值
取最大值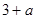 ,
,
所以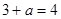 ,即
,即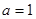 .
.
(3)先确定得到
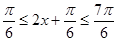 ,将
,将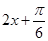 看作t,研究函数y=sint在
看作t,研究函数y=sint在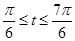 的最值情况。
的最值情况。解:(1)
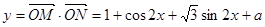 ,
,所以
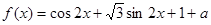 .
.(2)由(1)可得
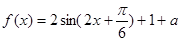 ,
,由
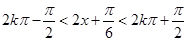 , 解得
, 解得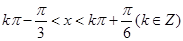 ;
;由
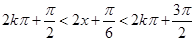 , 解得
, 解得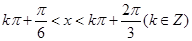 ,
,所以
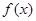 的单调递增区间为
的单调递增区间为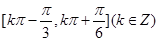 ,
,单调递减区间为
 .
.(3)
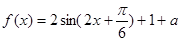 ,因为
,因为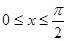 , 所以
, 所以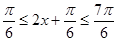 ,
,当
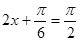 ,即
,即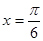 时,
时,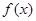 取最大值
取最大值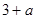 ,
,所以
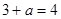 ,即
,即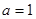 .
.
练习册系列答案
相关题目
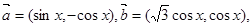 设函数
设函数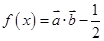 ;
; 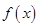 的单调递增区间;
的单调递增区间;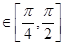 求函数
求函数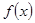 的最值及对应的x的值;
的最值及对应的x的值;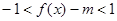 在x
在x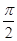 ,j=
,j=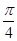
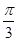 ,j=
,j=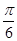
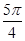
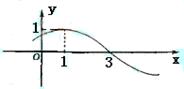

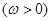 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为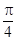 .
.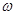 值;(2)若
值;(2)若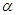 是第四象限角,
是第四象限角,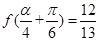 ,求
,求 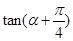 的值
的值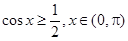 ,且
,且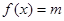 有且仅有一个实根,求实数
有且仅有一个实根,求实数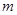 的值.
的值.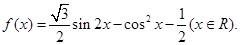
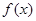 的最小值和最小正周期;
的最小值和最小正周期;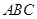 的内角
的内角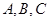 对边分别为
对边分别为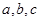 ,且
,且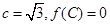 ,若
,若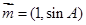 与
与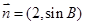 共线,求
共线,求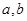 的值.
的值.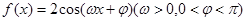 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移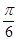 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2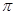 的奇函数
的奇函数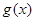 .
.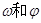 的值;
的值;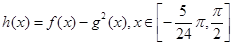 的单调区间和最值.
的单调区间和最值. ~
~ 时的温度变化曲线近似满足函数
时的温度变化曲线近似满足函数  .则中午12点时最接近的温度为:( )
.则中午12点时最接近的温度为:( )




 ( )
( )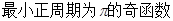



 的最大值和最小值分别为
的最大值和最小值分别为 ,则
,则