题目内容
18.一长方体,其长、宽、高分别为3,1,$\sqrt{6}$,则该长方体的外接球的表面积是( )| A. | 16π | B. | 64π | C. | $\frac{32π}{3}$ | D. | $\frac{252π}{3}$ |
分析 长方体的对角线就是外接球的直径,求出长方体的对角线长,即可求出球的半径,再求球的表面积.
解答 解:由题意长方体的对角线就是球的直径,
所以长方体的对角线长为:$\sqrt{9+1+6}$=4,
所以球的直径为:4,半径为:2,
球的表面积是:4πr2=16π.
故选A.
点评 本题是基础题,考查长方体的外接球的半径的求法、球内接多面体、球的体积和表面积,考查计算能力和空间想象能力.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
9.过椭圆的右焦点F2作椭圆长轴的垂线交椭圆于A,B两点,F1为椭圆的左焦点,若△F1AB为正三角形,则椭圆的离心率为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2-$\sqrt{3}$ | D. | $\sqrt{2}$-1 |
6.在复平面内,复数 z=3+4i 则 z 的共轭复数的模为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 25 |
3.已知 m,n 表示两条不同直线,α表示平面.下列说法正确的是( )
| A. | 若 m∥α,n∥α,则 m∥n | B. | 若 m⊥α,n?α,则 m⊥n | ||
| C. | 若 m⊥α,m⊥n,则 n∥α | D. | 若 m∥α,m⊥n,则 n⊥α |
10.命题“?x>0,$\frac{x-2}{x}$≥0”的否定是( )
| A. | ?x≤0,$\frac{x-2}{x}$<0 | B. | ?x>0,$\frac{x-2}{x}$<0 | C. | ?x>0,0≤x<2 | D. | ?x>0,0<x<2 |
7.已知函数y=f(x),下列说法错误的是( )
| A. | △y=f(x0+△x)-f(x0)叫函数值的改变量 | |
| B. | $\frac{△y}{△x}$=$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$叫该函数在[x0,x0+△x]上的平均变化率 | |
| C. | f(x)在点x0处的导数记为y′ | |
| D. | f(x)在点x0处的导数记为f′(x0) |
8.若函数$f(x)=|{{{log}_a}x}|-{2^{-x}}({a>0,a≠1})$的两个零点是m,n,则( )
| A. | mn=1 | B. | mn>1 | C. | mn<1 | D. | 以上都不对 |
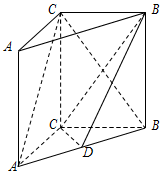 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.求证:
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.求证: