题目内容
7.已知函数y=f(x),下列说法错误的是( )| A. | △y=f(x0+△x)-f(x0)叫函数值的改变量 | |
| B. | $\frac{△y}{△x}$=$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$叫该函数在[x0,x0+△x]上的平均变化率 | |
| C. | f(x)在点x0处的导数记为y′ | |
| D. | f(x)在点x0处的导数记为f′(x0) |
分析 根据题意,依次分析选项,是否符合导数的定义,即可得答案.
解答 解:根据题意,依次分析选项:
对于A、△y=f(x0+△x)-f(x0)叫函数值的改变量,正确;
对于B、$\frac{△y}{△x}$=$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$叫该函数在[x0,x0+△x]上的平均变化率,正确;
对于C、f(x)在点x0处的导数记为f′(x0),y′表示函数y=f(x)的导数,错误;
对于D、f(x)在点x0处的导数记为f′(x0),正确;
故选:C.
点评 本题考查导数的定义,关键是掌握导数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一长方体,其长、宽、高分别为3,1,$\sqrt{6}$,则该长方体的外接球的表面积是( )
| A. | 16π | B. | 64π | C. | $\frac{32π}{3}$ | D. | $\frac{252π}{3}$ |
15.已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有$f[{f(x)+{{log}_{\frac{1}{3}}}x}]=4$,且方程|f(x)-3|=x3-6x2+9x-4+a在区间[0,3]上有两解,则实数a的取值范围是( )
| A. | 0<a≤5 | B. | a<5 | C. | 0<a<5 | D. | a≥5 |
12.如果a>b>0,那么下面一定成立的是( )
| A. | a-b<0 | B. | ac>bc | C. | $\frac{1}{a}$<$\frac{1}{b}$ | D. | a3<b3 |
16.已知命题p:?x∈R,ax2+2x+3>0.若命题p为假命题,则实数a的取值范围是( )
| A. | {a|a<$\frac{1}{3}$} | B. | {a|0<a≤$\frac{1}{3}$} | C. | {a|a≤$\frac{1}{3}$} | D. | {a|a≥$\frac{1}{3}$} |
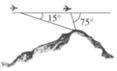 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.