题目内容
(本小题满分14分)如图,在四棱柱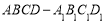 中,
中,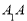
 底面
底面 ,
,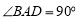 ,
,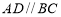 ,且
,且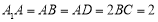 ,点E在棱AB上,平面
,点E在棱AB上,平面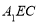 与棱
与棱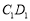 相交于点F.
相交于点F.

(Ⅰ)证明: ∥平面
∥平面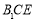 ;
;
(Ⅱ)若E是棱AB的中点,求二面角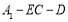 的余弦值;
的余弦值;
(Ⅲ)求三棱锥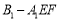 的体积的最大值.
的体积的最大值.
(Ⅰ)详见解析; (Ⅱ)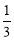 ;(Ⅲ)
;(Ⅲ) .
.
【解析】
试题分析:(Ⅰ)证明:因为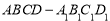 是棱柱,所以平面
是棱柱,所以平面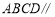 平面
平面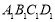 ,由面面平行的性质定理可知,
,由面面平行的性质定理可知,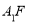 ∥
∥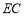 .根据线面平行的判定定理,即可证明结果.
.根据线面平行的判定定理,即可证明结果.
(Ⅱ)因为
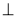 底面
底面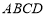 ,
,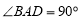 ,所以
,所以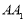 ,
,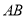 ,
,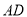 两两垂直,以A为原点,以
两两垂直,以A为原点,以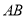 ,
,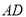 ,
,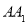 分别为
分别为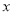 轴、
轴、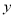 轴和
轴和 轴,如图建立空间直角坐标系. 利用空间向量在立体几何中的应用,求出平面
轴,如图建立空间直角坐标系. 利用空间向量在立体几何中的应用,求出平面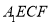 的法向量为
的法向量为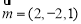 又因为平面
又因为平面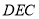 的法向量为
的法向量为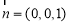 , 根据向量的夹角公式,即可求出二面角
, 根据向量的夹角公式,即可求出二面角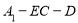 的余弦值;
的余弦值;
(Ⅲ)过点F作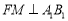 于点
于点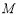 ,因为平面
,因为平面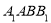
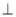 平面
平面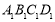 ,
,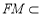 平面
平面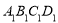 ,所以
,所以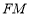
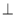 平面
平面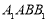 ,所以
,所以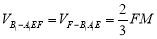 ,因为当F与点
,因为当F与点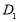 重合时,
重合时,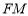 取到最大值2(此时点E与点B重合),即可求出三棱锥
取到最大值2(此时点E与点B重合),即可求出三棱锥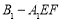 的体积的最大值.
的体积的最大值.
试题解析:(Ⅰ)证明:因为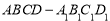 是棱柱,
是棱柱,
所以平面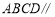 平面
平面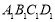 .
.
又因为平面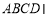 平面
平面 ,平面
,平面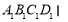 平面
平面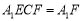 ,
,
所以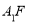 ∥
∥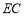 . 2分
. 2分
又因为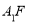
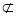 平面
平面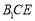 ,
,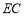
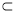 平面
平面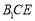 ,
,
所以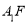 ∥平面
∥平面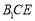 . 4分
. 4分
(Ⅱ)【解析】
因为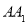
 底面
底面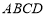 ,
,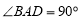 ,
,
所以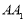 ,
,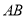 ,
,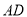 两两垂直,以A为原点,以
两两垂直,以A为原点,以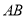 ,
,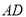 ,
,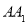 分别为
分别为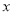 轴、
轴、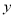 轴和
轴和 轴,如图建立空间直角坐标系. 5分
轴,如图建立空间直角坐标系. 5分
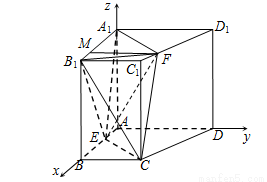
则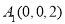 ,
,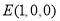 ,
,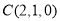 ,
,
所以 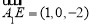 ,
,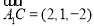 .
.
设平面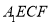 的法向量为
的法向量为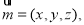
由 ,
,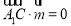 ,
,
得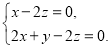
令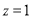 ,得
,得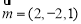 . 7分
. 7分
又因为平面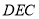 的法向量为
的法向量为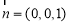 , 8分
, 8分
所以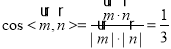 ,
,
由图可知,二面角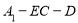 的平面角为锐角,
的平面角为锐角,
所以二面角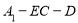 的余弦值为
的余弦值为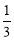 . 10分
. 10分
(Ⅲ)【解析】
过点F作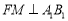 于点
于点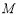 ,
,
因为平面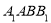
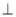 平面
平面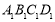 ,
,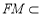 平面
平面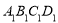 ,
,
所以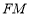
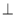 平面
平面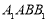 ,
,
所以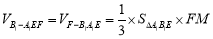 12分
12分
 .
.
因为当F与点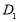 重合时,
重合时,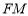 取到最大值2(此时点E与点B重合),
取到最大值2(此时点E与点B重合),
所以当F与点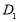 重合时,三棱锥
重合时,三棱锥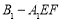 的体积的最大值为
的体积的最大值为 . 14分.
. 14分.
考点: 1.线面平行的判定定理和性质定理;2.空间向量在立体几何中的应用;3.锥体的体积公式.

 高中必刷题系列答案
高中必刷题系列答案
 ,则
,则 ______.
______. :
: ,则
,则 为( )
为( )



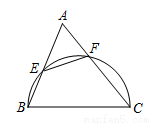
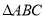 中,以
中,以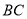 为直径的半圆分别交
为直径的半圆分别交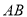 ,
,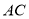 于点
于点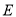 ,
,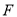 ,且
,且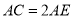 ,那么____;
,那么____; ___.
___.
 ,
,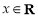 ,则“
,则“ ”是“函数
”是“函数 为奇函数”的( )
为奇函数”的( ) 中,
中,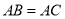 ,
,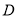 在线段
在线段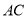 ,
,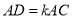 (
(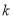 为常数,且
为常数,且 ),
), 为定长,则
为定长,则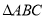 的面积最大值为( )
的面积最大值为( ) B.
B. C.
C.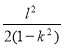 D.
D.
 、
、 R,且
R,且 ,则( )
,则( ) B.
B.
 D.
D.