题目内容
(本小题共14分)已知椭圆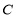 的中心在原点,焦点在
的中心在原点,焦点在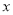 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为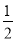 .
.
(Ⅰ)求椭圆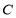 的标准方程;
的标准方程;
(Ⅱ)设直线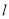 经过点
经过点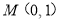 ,且与椭圆
,且与椭圆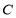 交于
交于 两点,若
两点,若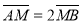 ,求直线
,求直线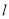 的方程.
的方程.
(Ⅰ)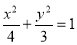 (Ⅱ)
(Ⅱ)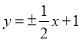
【解析】
试题分析:(Ⅰ)由椭圆焦距为2 得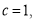 ,由离心率是
,由离心率是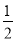 得
得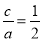 ,另外结合
,另外结合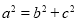 列方程组即可确定
列方程组即可确定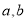 的值从而得到椭圆C的方程;(Ⅱ)设
的值从而得到椭圆C的方程;(Ⅱ)设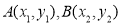 ,先讨论当k不存在时,直线方程为
,先讨论当k不存在时,直线方程为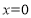 ,不符合题意.再研究当k存在时,设直线方程为
,不符合题意.再研究当k存在时,设直线方程为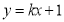 ,将直线方程与椭圆方程联立消去一个变量,得到关于
,将直线方程与椭圆方程联立消去一个变量,得到关于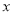 的一元二次方程,结合一元二次方程根的判别式与韦达定理以及由
的一元二次方程,结合一元二次方程根的判别式与韦达定理以及由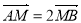 ,则
,则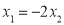 ,确定的关系,从而求出实数
,确定的关系,从而求出实数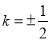 .所求直线方程为
.所求直线方程为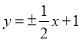 .
.
试题解析:(Ⅰ)由题意知, 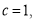 1分
1分
解得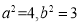 3分
3分
故椭圆方程为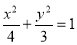 . 4分
. 4分
(Ⅱ)设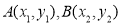
当k不存在时,直线方程为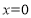 ,不符合题意. 5分
,不符合题意. 5分
当k存在时,设直线方程为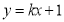 ,
,
联立 ,消去
,消去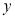 ,得:
,得: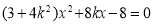 , 6分
, 6分
由题意,点在椭圆内部,必有两个交点,方程必有实根.(或计算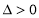 ) 7分
) 7分
 8分
8分
若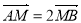 ,则
,则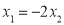 , 9分
, 9分
代入上式,可得
 ,消去
,消去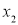 ,解得
,解得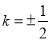 . 13分
. 13分
所求直线方程为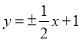 . 14分
. 14分
考点:椭圆方程,直线与椭圆位置关系

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.4
B.4 D.2
D.2
 ,则y=( )
,则y=( ) 的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( )
的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( ) 和点
和点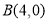 到直线
到直线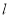 的距离依次为1和2,则这样的直线有( )
的距离依次为1和2,则这样的直线有( ) 为等差数列,
为等差数列, ,公差
,公差 ,
, 、
、 、
、 成等比数列,则
成等比数列,则
 的部分图象如图所示,则( )
的部分图象如图所示,则( )
 B.
B.
 D.
D.