题目内容
(本题满分12分)
已知函数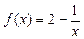 ,数列
,数列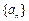 满足
满足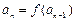 (n≥2,nÎN*).
(n≥2,nÎN*).
若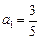 ,数列
,数列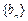 满足
满足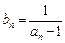
(1)求证:数列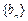 是等差数列;
是等差数列;
(2)设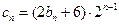 ,求数列
,求数列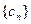 的前n项和
的前n项和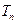 。
。
已知函数
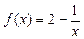 ,数列
,数列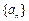 满足
满足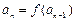 (n≥2,nÎN*).
(n≥2,nÎN*).若
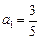 ,数列
,数列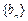 满足
满足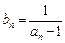
(1)求证:数列
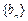 是等差数列;
是等差数列;(2)设
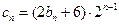 ,求数列
,求数列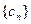 的前n项和
的前n项和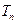 。
。(1)略;(2)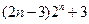
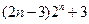
由已知得: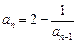 (n≥2,nÎN*). …………………2分
(n≥2,nÎN*). …………………2分
(1)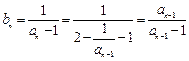 ,
,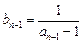 , ……………4分
, ……………4分
∴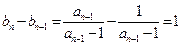 (n≥2,nÎN*).
(n≥2,nÎN*).
∴数列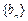 是等差数列. ……………6分
是等差数列. ……………6分
(2)由(1)知,数列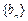 是等差数列,首项
是等差数列,首项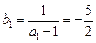 ,公差为1,
,公差为1,
则其通项公式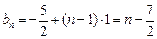 , ……………8分
, ……………8分
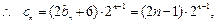 ……………10分
……………10分
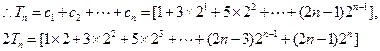
两式相减得
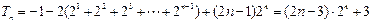
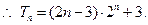 …………………………12分
…………………………12分
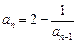 (n≥2,nÎN*). …………………2分
(n≥2,nÎN*). …………………2分(1)
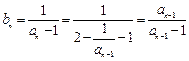 ,
,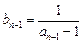 , ……………4分
, ……………4分∴
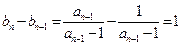 (n≥2,nÎN*).
(n≥2,nÎN*).∴数列
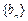 是等差数列. ……………6分
是等差数列. ……………6分(2)由(1)知,数列
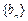 是等差数列,首项
是等差数列,首项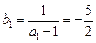 ,公差为1,
,公差为1,则其通项公式
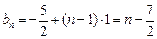 , ……………8分
, ……………8分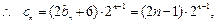 ……………10分
……………10分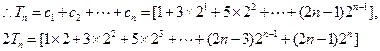
两式相减得
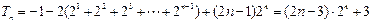
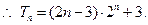 …………………………12分
…………………………12分
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
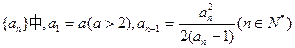
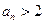 ;
;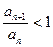 ;
;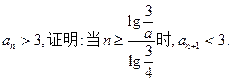
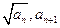 )(n
)(n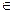 N*)在函数y=x2+1的图象上。 (Ⅰ)求数列{an}的通项公式;
N*)在函数y=x2+1的图象上。 (Ⅰ)求数列{an}的通项公式;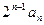 (n∈N*),求数列{bn}的前n项和
(n∈N*),求数列{bn}的前n项和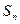 。
。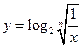
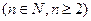
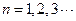 时,把已知函数的图像与直线
时,把已知函数的图像与直线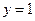 的交点的横坐标依次为
的交点的横坐标依次为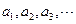 求证:
求证: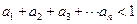
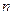 的值,设
的值,设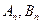 为已知函数的图上与
为已知函数的图上与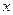 轴距离为1的两点,求证:
轴距离为1的两点,求证: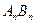 为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。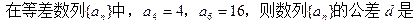 ( )
( )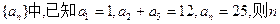 为 ( )
为 ( )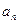 }的公比q≠1,且
}的公比q≠1,且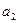 ,
,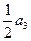 ,
,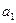 成等差数列,则
成等差数列,则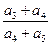 的值为( )
的值为( )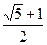
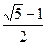
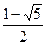
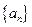 满足
满足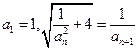 ,记
,记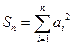 ,若
,若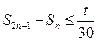 对任意的
对任意的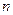
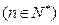 恒成立,则正整数
恒成立,则正整数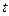 的最小值为 ( )
的最小值为 ( )