题目内容
已知函数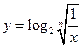
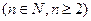
(1)当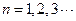 时,把已知函数的图像与直线
时,把已知函数的图像与直线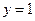 的交点的横坐标依次为
的交点的横坐标依次为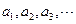 求证:
求证: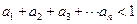
(2)对于每一个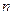 的值,设
的值,设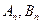 为已知函数的图上与
为已知函数的图上与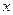 轴距离为1的两点,求证:
轴距离为1的两点,求证: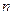 取任意一个正数时,以
取任意一个正数时,以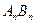 为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
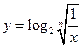
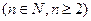
(1)当
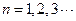 时,把已知函数的图像与直线
时,把已知函数的图像与直线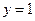 的交点的横坐标依次为
的交点的横坐标依次为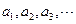 求证:
求证: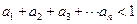
(2)对于每一个
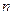 的值,设
的值,设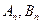 为已知函数的图上与
为已知函数的图上与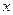 轴距离为1的两点,求证:
轴距离为1的两点,求证: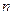 取任意一个正数时,以
取任意一个正数时,以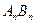 为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。(1)略
(2)以C为圆心,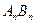 为直径的圆必与定直线y轴相切,故是直线方程是
为直径的圆必与定直线y轴相切,故是直线方程是 ,切点坐标为(0, 0)
,切点坐标为(0, 0)
(2)以C为圆心,
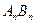 为直径的圆必与定直线y轴相切,故是直线方程是
为直径的圆必与定直线y轴相切,故是直线方程是 ,切点坐标为(0, 0)
,切点坐标为(0, 0)原函数可化为 (1)
(1) 时,
时,

 是首项和公比均为
是首项和公比均为 的等比数列
的等比数列



(2)由题设得: 解得
解得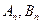 的坐标分别为
的坐标分别为 ,
,



 的中点C到y轴的距离为
的中点C到y轴的距离为
综上,以C为圆心,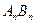 为直径的圆必与定直线y轴相切,故是直线方程是
为直径的圆必与定直线y轴相切,故是直线方程是 ,切点坐标为(0, 0).
,切点坐标为(0, 0).
 (1)
(1) 时,
时,

 是首项和公比均为
是首项和公比均为 的等比数列
的等比数列



(2)由题设得:
 解得
解得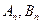 的坐标分别为
的坐标分别为 ,
,



 的中点C到y轴的距离为
的中点C到y轴的距离为
综上,以C为圆心,
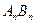 为直径的圆必与定直线y轴相切,故是直线方程是
为直径的圆必与定直线y轴相切,故是直线方程是 ,切点坐标为(0, 0).
,切点坐标为(0, 0).
练习册系列答案
相关题目
 中,
中,
 ,证明:数列
,证明:数列 是等差数列
是等差数列 项和
项和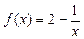 ,数列
,数列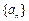 满足
满足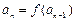 (n≥2,nÎN*).
(n≥2,nÎN*).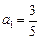 ,数列
,数列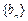 满足
满足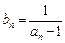
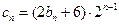 ,求数列
,求数列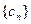 的前n项和
的前n项和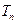 。
。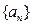 是等差数列,其前n项和为
是等差数列,其前n项和为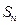 ,已知
,已知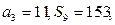 求数列
求数列

 ,
, ,
, ,则项数
,则项数 为
为 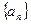 的前
的前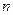 项和为
项和为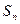 ,若
,若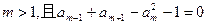 ,
,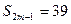 ,则
,则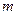 等于 ( )
等于 ( ) ﹜为等差数列,且
﹜为等差数列,且 ,则
,则 的值为___________.
的值为___________. %,到期时净得本金和利息共计
%,到期时净得本金和利息共计 元,则利息税的税率是( )
元,则利息税的税率是( )