题目内容
已知数列 满足
满足 ,
, .
.
(1)若 为递增数列,且
为递增数列,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)若 ,且
,且 是递增数列,
是递增数列, 是递减数列,求数列
是递减数列,求数列 的通项公式.
的通项公式.
 满足
满足 ,
, .
.(1)若
 为递增数列,且
为递增数列,且 成等差数列,求
成等差数列,求 的值;
的值;(2)若
 ,且
,且 是递增数列,
是递增数列, 是递减数列,求数列
是递减数列,求数列 的通项公式.
的通项公式.(1)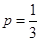 (2)
(2) 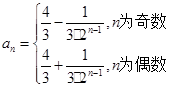 或
或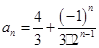
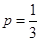 (2)
(2) 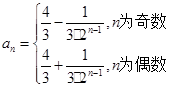 或
或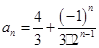
试题分析:(1)利用数列
 的单调性,得到
的单调性,得到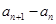 的符号去掉
的符号去掉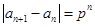 的绝对值,再分布令
的绝对值,再分布令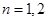 得到
得到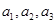 之间的关系,再利用题目已知等差中项的性质列出关于
之间的关系,再利用题目已知等差中项的性质列出关于 的等式,即可求出
的等式,即可求出 的值.
的值.(2)根据数列
 在
在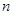 为奇数和偶数的单调性可得到
为奇数和偶数的单调性可得到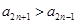 且
且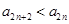 ,两不等式变为同号相加即可得到
,两不等式变为同号相加即可得到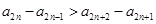 ,根据题意可得
,根据题意可得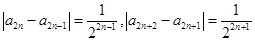 结合
结合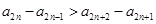 与
与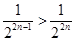 可去掉
可去掉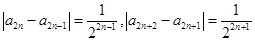 的绝对值,分
的绝对值,分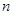 为奇或偶数,利用叠加法即可求出数列
为奇或偶数,利用叠加法即可求出数列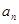 的通项公式.
的通项公式.(1)因为数列
 为递增数列,所以
为递增数列,所以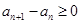 ,则
,则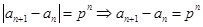 ,分别令
,分别令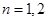 可得
可得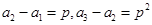
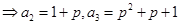 ,因为
,因为 成等差数列,所以
成等差数列,所以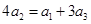
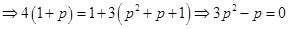
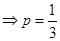 或
或 ,
,当
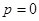 时,数列
时,数列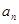 为常数数列不符合数列
为常数数列不符合数列 是递增数列,所以
是递增数列,所以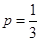 .
.(2)由题可得
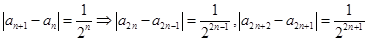 ,因为
,因为 是递增数列且
是递增数列且 是递减数列,所以
是递减数列,所以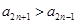 且
且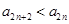 ,则有
,则有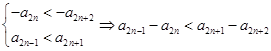 ,因为
,因为(2)由题可得
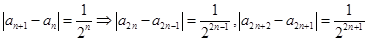 ,因为
,因为 是递增数列且
是递增数列且 是递减数列,所以
是递减数列,所以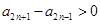 且
且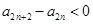
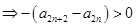 ,两不等式相加可得
,两不等式相加可得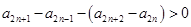
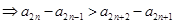 ,
,又因为
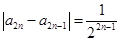
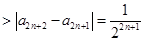 ,所以
,所以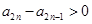 ,即
,即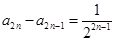 ,
,同理可得
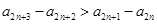 且
且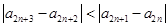 ,所以
,所以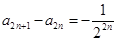 ,
,则当
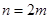
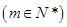 时,
时,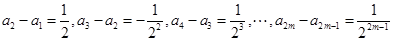 ,这
,这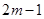 个等式相加可得
个等式相加可得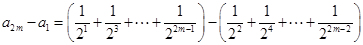
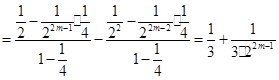
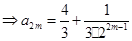 .
.当
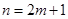 时,
时, 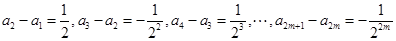 ,这
,这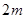 个等式相加可得
个等式相加可得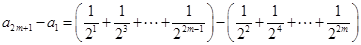
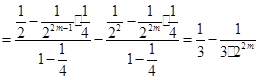
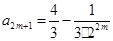 ,当
,当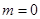 时,
时,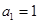 符合,故
符合,故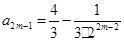
综上
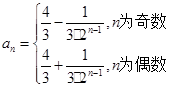 .
.
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
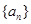 的前n项和
的前n项和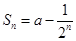 ,(1)求实数
,(1)求实数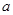 的值;(2)求数列
的值;(2)求数列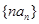 的前n项和
的前n项和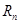 .
. 中,
中, ,则
,则 ( )
( ) 满足
满足
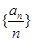 是等差数列;
是等差数列;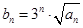 ,求数列
,求数列 的前
的前 项和
项和
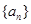 满足
满足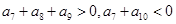 ,则当
,则当 时,
时,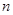 项和最大.
项和最大.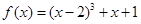 ,数列
,数列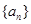 是公差不为0的等差数列,
是公差不为0的等差数列,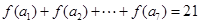 ,则
,则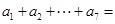 。
。 满足
满足 且
且 成等比数列,则
成等比数列,则 .
.