Question

6．在平行四边形ABCD中，对角线AC与BD交于点O，M为平行四边形ABCD所在平面内任意一点，给出如下结论：
①$\overrightarrow{AB}$+$\overrightarrow{AD}$=2$\overrightarrow{AO}$
②$\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$+$\overrightarrow{MD}$=4$\overrightarrow{OM}$
③若M∈AB，则满足x²$\overrightarrow{OA}$+2x$\overrightarrow{OM}$+$\overrightarrow{OB}$=$\overrightarrow{0}$的实数x有无数个
④若M∈AB，且满足x²$\overrightarrow{OA}$+2x$\overrightarrow{OM}$+$\overrightarrow{OB}$=$\overrightarrow{0}$，则点M是AB的中点．
其中正确的结论是①④（填上你认为正确的所有结论序号）

Answer 1

分析 可作出图形，根据向量加法的平行四边形法则及加法的几何意义即可判断①②的正误，对于③④，可以根据条件得到$x\overrightarrow{OA}+\overrightarrow{OM}=\frac{1}{2x}\overrightarrow{BO}$，然后根据向量加法的平行四边形法及平行线分线段成比例定理便可得到$1-\frac{1}{-2x}=-\frac{x}{2}$，可解出x=-1，这样即可判断结论④正确．

解答 解：如图，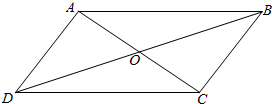

①$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}=2\overrightarrow{AO}$，该结论正确；
②$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}$=$（\overrightarrow{MO}+\overrightarrow{OA}）+（\overrightarrow{MO}+\overrightarrow{OB}）$$+（\overrightarrow{MO}+\overrightarrow{OC}）+（\overrightarrow{MO}+\overrightarrow{OD}）$=$4\overrightarrow{MO}+（\overrightarrow{OA}+\overrightarrow{OC}）+（\overrightarrow{OB}+\overrightarrow{OD}）$=$4\overrightarrow{MO}$，∴该结论错误；
③根据条件知，x≠0，∴$\frac{x}{2}\overrightarrow{OA}+\overrightarrow{OB}=\frac{1}{2x}\overrightarrow{BO}$，x＜0，如图，作MN∥AC，NE∥OM，分别交OB于N，OC于E；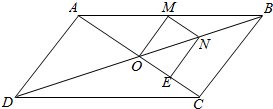

则$ON=\frac{1}{-2x}OB$，$OE=MN=-\frac{x}{2}AO$；
∴$1-\frac{1}{-2x}=-\frac{x}{2}$；
∴解得x=-1；
∴$MN=\frac{1}{2}AO$；
∴M为AB的中点；
∴③错误，④正确；
∴正确的结论为①④．
故答案为：①④．

点评 考查向量加法的平行四边形法则，向量加法的几何意义，以及共线向量基本定理，平行线分线段成比例定理．