题目内容
已知 ,O为极点,则使△POP′是正三角形的P′点的极坐标 .(规定ρ≥0,0≤θ<2π)
,O为极点,则使△POP′是正三角形的P′点的极坐标 .(规定ρ≥0,0≤θ<2π)
【答案】分析:求出P的直角坐标,利用∠POP′=60°,OP=OP′,得到①和②,解方程组求得m,n,即得P′的直角坐标,再把直角坐标化为极坐标.
解答:解:P的直角坐标为 (5cos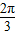 ,5sin
,5sin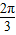 ),即 (
),即 (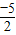 ,
,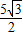 ).当△POP′是正三角形时,
).当△POP′是正三角形时,
设P(m,n ),则∠POP′=60°,OP=OP′=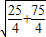 =5. 故有
=5. 故有
tan60°=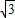 =
=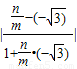 ①,且
①,且 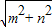 =5 ②.
=5 ②.
由①②解得 m=-5 且n=0,或 m= ,n=
,n=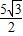 ,即P(-5,0),或 P(
,即P(-5,0),或 P(  ,
,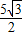 ),
),
根据ρ=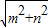 和 tanθ=
和 tanθ=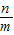 ,求得P′的极坐标(ρ,θ ).
,求得P′的极坐标(ρ,θ ).
故P′点的极坐标为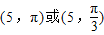 ,
,
故答案为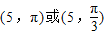 .
.
点评:本题考查极坐标与直角坐标的互化,两条直线的夹角公式,两点间的距离公式,列出①②是解题的关键.
解答:解:P的直角坐标为 (5cos
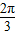 ,5sin
,5sin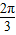 ),即 (
),即 (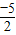 ,
,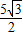 ).当△POP′是正三角形时,
).当△POP′是正三角形时,设P(m,n ),则∠POP′=60°,OP=OP′=
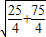 =5. 故有
=5. 故有tan60°=
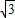 =
=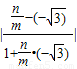 ①,且
①,且 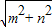 =5 ②.
=5 ②.由①②解得 m=-5 且n=0,或 m=
 ,n=
,n=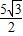 ,即P(-5,0),或 P(
,即P(-5,0),或 P(  ,
,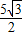 ),
),根据ρ=
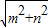 和 tanθ=
和 tanθ=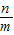 ,求得P′的极坐标(ρ,θ ).
,求得P′的极坐标(ρ,θ ).故P′点的极坐标为
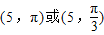 ,
,故答案为
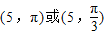 .
.点评:本题考查极坐标与直角坐标的互化,两条直线的夹角公式,两点间的距离公式,列出①②是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 ,O为极点,则使△POP′是正三角形的P′点的极坐标________.(规定ρ≥0,0≤θ<2π)
,O为极点,则使△POP′是正三角形的P′点的极坐标________.(规定ρ≥0,0≤θ<2π)