题目内容
已知P(5,
π),O为极点,则使△POP′是正三角形的P′点的极坐标______.(规定ρ≥0,0≤θ<2π)
| 2 |
| 3 |
P的直角坐标为 (5cos
,5sin
),即 (
,
).当△POP′是正三角形时,
设P(m,n ),则∠POP′=60°,OP=OP′=
=5. 故有
tan60°=
=|
| ①,且
=5 ②.
由①②解得 m=-5 且n=0,或 m=
,n=
,即P(-5,0),或 P(
,
),
根据ρ=
和 tanθ=
,求得P′的极坐标(ρ,θ ).
故P′点的极坐标为(5,π)或(5,
),
故答案为 (5,π)或(5,
).
| 2π |
| 3 |
| 2π |
| 3 |
| -5 |
| 2 |
5
| ||
| 2 |
设P(m,n ),则∠POP′=60°,OP=OP′=
|
tan60°=
| 3 |
| ||||
1+
|
| m2+ n2 |
由①②解得 m=-5 且n=0,或 m=
| 5 |
| 2 |
5
| ||
| 2 |
| 5 |
| 2 |
5
| ||
| 2 |
根据ρ=
| m2+n2 |
| n |
| m |
故P′点的极坐标为(5,π)或(5,
| π |
| 3 |
故答案为 (5,π)或(5,
| π |
| 3 |

练习册系列答案
相关题目
为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.根据表中数据,得到K2的观测值k=
≈4.844.则可以有 %的把握认为选修文科与性别有关系.
| 理科 | 文科 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
| 50×(13×20-10×7)2 |
| 23×27×20×30 |
为了判断高中学生选读文科是否与性别有关,现随机抽取50名学生,得到如下2×2列联表:
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025,根据表中数据,得到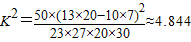 ,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.
,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.
| 理科 | 文科 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
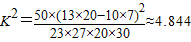 ,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.
,则在犯错误的概率不超过 的前提下可以认为选读文科与性别是有关系的.