题目内容
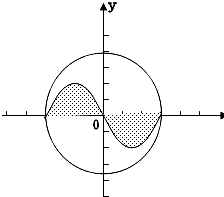圆x2+y2=π2内的曲线y=-sinx与 x轴围成的阴影部分区域记为M（如图），随机往圆内投掷一个点A，则点A落在区域M的概率为________．
分析：先求构成试验的全部区域为圆内的区域的面积，再利用积分知识可得正弦曲线y=sinx与x轴围成的区域的面积，从而可求概率．
解答：构成试验的全部区域为圆内的区域，面积为π3
正弦曲线y=-sinx与x轴围成的区域记为M，
根据图形的对称性得：面积为S=2∫0πsinxdx=-2cosx|0π=4，
由几何概率的计算公式可得，随机往圆O内投一个点A，则点A落在区域M内的概率P=
故答案为：
点评：本题考查利用积分求解曲面的面积，几何概型的计算公式的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
设椭圆
+
=1（a＞0，b＞0）的离心率e=
，右焦点F（c，0），方程ax2+bx-c=0的两个根分别为x1，x2，则点P（x1，x2）在（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| A、圆x2+y2=2内 |
| B、圆x2+y2=2上 |
| C、圆x2+y2=2外 |
| D、以上三种情况都有可能 |
圆x2+y2=π2内的曲线y=-sinx与 x轴围成的阴影部分区域记为M（如图），随机往圆内投掷一个点A，则点A落在区域M的概率为
（2009•大连二模）如图所示，若向圆x2+y2=2内随机投一点（该点落在圆x2+y2=2内任何一点是等可能的），则所投的点落在圆与y轴及曲线y=x2（x≥0）围成的阴影图形S内部的概率是（ ）