题目内容

将曲线x+y2=1绕原点逆时针旋转45°后，得到的曲线C方程为
 
．
考点：旋转变换
专题：选作题,矩阵和变换
分析：先确定
x=
2
2
(x′+y′)
y=
2
2
(y′-x′′)
，再代入x+y2=1，可得曲线C的方程．
解答： 解：由题设条件，M=
cos45°-sin45°
sin45°cos45°
=
2
2
-
2
2
2
2
2
2
，
由
2
2
-
2
2
2
2
2
2
x
y
=
x′
y′
，解得
x=
2
2
(x′+y′)
y=
2
2
(y′-x′′)
，
代入x+y2=1，可得曲线C的方程为x2+y2-2xy+
2
x+
2
y-2=0．
故答案为：x2+y2-2xy+
2
x+
2
y-2=0．
点评：本题主要考查了矩阵的应用，同时考查了旋转变换，属于基础题．
练习册系列答案
相关题目
设M（ρ1，θ1），N（ρ2，θ2）两点的极坐标同时满足下列关系：ρ1+ρ2=0，θ1+θ2=0，则M，N两点（位置关系） 关于
 
对称．
已知函数f（x）是定义在R上的奇函数，其中f（1）=0，且当x＞0时，有
xf′(x)-f(x)
x2
＞0，则不等式f（x）＞0的解集是
 
．
已知x＞0，y＞0，z＞0，x+2y+3z=3，那么（x+
1
4y
）2+（2y+
1
6z
）2+（3z+
1
2x
）2的最小值为
 
．
已知函数f（x）的定义域为R，若f（0）=0，且任意的x∈R都有：f（
x
3
）=
1
2
f（x）和f（1-x）=1-f（x）成立，则f（
1
3
）+f（
1
6
）=
 
．
已知正三棱锥P-ABC的底面边长为1，高为2，则其体积为
 
．
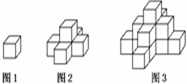如图1是一个水平摆放的小正方体木块，图2、图3是由这样的小正方体木块叠放而成，按照这样的规律继续逐个叠放下去，那么在第七个叠放的图形中小正方体木块数应是
 
．
复数z=i（1+i）（i是虚数单位）的共轭复数
.
z
在复平面内对应的点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
已知AD、BE分别是△ABC的边BC，AC上的中线，且
AD
=
a
，
BE
=
b
，则
BC
=（　　）
A、
1
3
a
+
2
3
b
B、
2
3
a
+
1
3
b
C、
2
3
a
+
4
3
b
D、
4
3
a
+
2
3
b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网