题目内容
16.已知点A(-1,0),点B(2,0),动点C满足|AC|=|AB|,则点C与点P(1,4)所连线段的中点M的轨迹方程为x2+(y-2)2=$\frac{9}{4}$.分析 求出点C的轨迹方程,利用中点公式得到点C与点P(1,4)的中点M的坐标关系,代入得到M的轨迹方程.
解答 解:因为A(-1,0)、点B(2,0),动点C满足|AC|=|AB|=3,
所以点C的轨迹为圆心为(-1,0)半径为3的圆,
方程为(x+1)2+y2=9.
设M(x,y),则C(2x-1,2y-4)
代入(x+1)2+y2=9,得到M的轨迹方程为x2+(y-2)2=$\frac{9}{4}$.
故答案为:x2+(y-2)2=$\frac{9}{4}$.
点评 本题考查圆的方程,考查代入法的运用,确定坐标之间的关系是关键.

练习册系列答案
相关题目
11.已知函数y=f(x)是定义在R上的奇函数,当x≤0时f(x)=2-x+m-1(m∈R),a=f(log45),b=(log23),c=f(m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
8.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | f(x)=$\frac{1}{1+{x}^{2}}$ | B. | f(x)=x2+x | C. | f(x)=cos$\frac{x}{3}$ | D. | f(x)=$\frac{2}{x}$ |
10.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )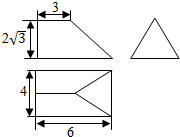

| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |