题目内容
在R上定义运算*:x*y=x•(1-y).若关于x的不等式x*(x-a)>0的解集是集合{x|-1≤x≤1}的子集,则实数a的取值范围是
- A.[0,2]
- B.[-2,-1)∪(-1,0]
- C.[0,1)∪(1,2]
- D.[-2,0]
D
分析:首先理解*运算的定义,得到不等式的具体形式,然后解不等式.不等式中有参数a,需要对参数的取值进行讨论,得到不等式的解集,然后再根据子集关系,确定出a的范围.值得注意的是不等式的解集有可能是空集,不可忘记.
解答:由题意得,x*(x-a)=x×[1-(x-a)]=x×[(a+1)-x],所以x*(x-a)>0,即:x×[x-(a+1)]<0,
由题意知该不等式的解集可以是空集,此时解得a=-1.
当不等式的解集不是空集时,分两种情况:
若a>-1,则解集为(0,a+1),又解集为(-1,1)的子集,所以a+1<1,即:a<0,故a的范围为(-1,0)
若a<-1,则解集为(a+1,0),又又解集为(-1,1)的子集,所以a+1>-1,即:a>-2,故a的范围为(-2,-1)
综上所述:a的范围为[-2,0],故选D.
点评:考查一元二次不等式的解法.
分析:首先理解*运算的定义,得到不等式的具体形式,然后解不等式.不等式中有参数a,需要对参数的取值进行讨论,得到不等式的解集,然后再根据子集关系,确定出a的范围.值得注意的是不等式的解集有可能是空集,不可忘记.
解答:由题意得,x*(x-a)=x×[1-(x-a)]=x×[(a+1)-x],所以x*(x-a)>0,即:x×[x-(a+1)]<0,
由题意知该不等式的解集可以是空集,此时解得a=-1.
当不等式的解集不是空集时,分两种情况:
若a>-1,则解集为(0,a+1),又解集为(-1,1)的子集,所以a+1<1,即:a<0,故a的范围为(-1,0)
若a<-1,则解集为(a+1,0),又又解集为(-1,1)的子集,所以a+1>-1,即:a>-2,故a的范围为(-2,-1)
综上所述:a的范围为[-2,0],故选D.
点评:考查一元二次不等式的解法.

练习册系列答案
相关题目
 :x
:x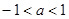 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.