题目内容
已知函数f(x)=
,x∈[0,
)
(1)若g(x)=f(x)+
,求g(x)的最小值及相应的x值
(2)若不等式(1-sinx)•f(x)>m(m-sinx)对于x∈[
,
]恒成立,求实数m的取值范围.
| 1+sinx |
| 1-sinx |
| π |
| 2 |
(1)若g(x)=f(x)+
| 1 |
| f(x) |
(2)若不等式(1-sinx)•f(x)>m(m-sinx)对于x∈[
| π |
| 6 |
| π |
| 4 |
考点:三角函数的最值,同角三角函数基本关系的运用
专题:计算题,三角函数的求值,三角函数的图像与性质,不等式的解法及应用
分析:(1)化简函数g(x)分离常数,得到-2+
,由x的范围,得到sin2x∈[0,1),即可得到函数的最小值和自变量x的值;
(2)将不等式化简得到(m+1)sinx-m2+1>0,令sinx=t,求得t∈[
,
].即不等式(m+1)t-m2+1>0对于x∈[
,
]恒成立,代入
,
得到两个二次不等式,解出它们,再求交集即可.
| 4 |
| 1-sin2x |
(2)将不等式化简得到(m+1)sinx-m2+1>0,令sinx=t,求得t∈[
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
解答:
解:(1)∵f(x)=
,x∈[0,
),
∴g(x)=f(x)+
=
+
=
=
=-2+
,
∵sinx∈[0,1),∴sin2x∈[0,1),
故当sin2x=0时,即x=0时,g(x)取最小值-2+4=2;
(2)不等式(1-sinx)•f(x)>m(m-sinx)即为1+sinx>m2-msinx,
即有(m+1)sinx-m2+1>0,
令sinx=t,由于x∈[
,
],则t∈[
,
].
由于不等式(m+1)t-m2+1>0对于x∈[
,
]恒成立,
则
(m+1)-m2+1>0,
(m+1)-m2+1>0.
解得-1<m<
且-1<m<1+
,
则m的取值范围是:(-1,
).
| 1+sinx |
| 1-sinx |
| π |
| 2 |
∴g(x)=f(x)+
| 1 |
| f(x) |
| 1+sinx |
| 1-sinx |
| 1-sinx |
| 1+sinx |
| (1+sinx)2+(1-sinx)2 |
| 1-sin2x |
| 2(1+sin2x) |
| 1-sin2x |
| 4 |
| 1-sin2x |
∵sinx∈[0,1),∴sin2x∈[0,1),
故当sin2x=0时,即x=0时,g(x)取最小值-2+4=2;
(2)不等式(1-sinx)•f(x)>m(m-sinx)即为1+sinx>m2-msinx,
即有(m+1)sinx-m2+1>0,
令sinx=t,由于x∈[
| π |
| 6 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
由于不等式(m+1)t-m2+1>0对于x∈[
| π |
| 6 |
| π |
| 4 |
则
| 1 |
| 2 |
| ||
| 2 |
解得-1<m<
| 3 |
| 2 |
| ||
| 2 |
则m的取值范围是:(-1,
| 3 |
| 2 |
点评:本题考查三角函数的化简和求值,考查正弦函数的最值和单调性,考查二次不等式的解法,考查转化思想的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
把119化成五进制数的末位数字为( )
| A、1 | B、2 | C、3 | D、4 |
直线l:3x-y-6=0被圆C:x2+y2-2x-4y=0截得的弦AB的长是( )
| A、10 | ||||
| B、5 | ||||
C、
| ||||
D、
|
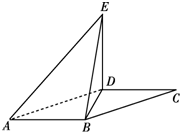 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.