题目内容
已知A(0,-4),B(3,2),抛物线y2=8x上的点到直线AB的最短距离为 .
【答案】分析:用两点式求得直线AB的方程为 2x-y-4=0,设抛物线y2=8x上的点P(t,t2),求得点P到直线AB的距离 d=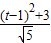 ≥
≥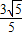 ,从而得出结论.
,从而得出结论.
解答:解:用两点式求得直线AB的方程为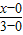 =
=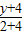 ,即2x-y-4=0,
,即2x-y-4=0,
设抛物线y2=8x上的点P(t,t2),则点P到直线AB的距离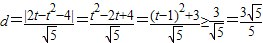 ,
,
故答案为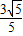 .
.
点评:本题主要考查用两点式求直线的方程,点到直线的距离公式、二次函数的性质的应用,属于中档题.
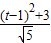 ≥
≥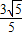 ,从而得出结论.
,从而得出结论.解答:解:用两点式求得直线AB的方程为
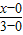 =
=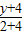 ,即2x-y-4=0,
,即2x-y-4=0,设抛物线y2=8x上的点P(t,t2),则点P到直线AB的距离
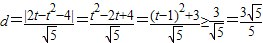 ,
,故答案为
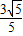 .
.点评:本题主要考查用两点式求直线的方程,点到直线的距离公式、二次函数的性质的应用,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目