题目内容
若f（x）=3sin（2x+?）+a，对任意实数x都有f(
+x)=f(
-x)，且f(
)=-4，则实数a的值等于（ ）
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
分析：利用对任意实数t都有f(
+x)=f(
-x)得到x=
为f（x）的对称轴，得到f（
）为最大值或最小值，得到3+a=-4或-3+a=-4求出a的值．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：解：因为对任意实数t都有f(
+x)=f(
-x)，
所以x=
为f（x）的对称轴，
所以f（
）为最大值或最小值，
所以3+a=-4或-3+a=-4
所以a=-7或a=-1
故选B．
| π |
| 3 |
| π |
| 3 |
所以x=
| π |
| 3 |
所以f（
| π |
| 3 |
所以3+a=-4或-3+a=-4
所以a=-7或a=-1
故选B．
点评：本题考查抽象函数的应用，在解决三角函数的性质问题时，一般先化简三角函数，然后利用整体角处理的方法来解决．
练习册系列答案
相关题目
，且
，则实数a的值等于
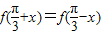，且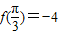
，则实数a的值等于（ ）