题目内容
3．
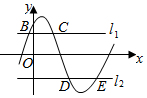（理）如图，直线l1：y=m（0＜m≤A）与函数f（x）=Acos（ωx+φ）（A＞0，ω＞0）的图象相交于B、C两点，直线l2：y=-m与函数f（x）=Acos（ωx+φ）（A＞0，ω＞0）的图象相交于D、E两点，设B（xB，yB），D（x，yD），记S（m）=|xB-xD|，则S（m）的图象大致是（ ）| A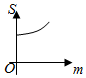． |  | B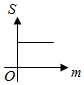． |  | C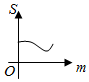． |  | D． |  |
分析 根据三角函数既是轴对称图形，又是中心对称图形的特点分析四点的对称关系，得出结论．
解答 
解：设B，C两点关于直线x=a对称，D，E两点关于直线x=b对称，f（x）的最小正周期为T，
则b-a=$\frac{1}{2}$T，
∵f（x）图象是中心对称图形，设f（x）的对称中心为（c，0），
则xE=2c-xB，xD=2c-xC，
∴xE-xD=xC-xB，
∵f（x）是轴对称图形，
∴a-xB=b-xD，
∴|xB-xD|=b-a=$\frac{1}{2}$T，
故S（m）是常数函数，
故选B．
点评 本题考查了三角函数的图象与性质，属于中档题．
练习册系列答案
初中学业考试导与练系列答案
相关题目
设椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的长轴长为6，离心率$e=\frac{{\sqrt{6}}}{3}$，O为坐标原点．
11．设f（x）是定义在R上周期为2的奇函数，当0≤x≤1时，f（x）=x2-x，则$f（{-\frac{5}{2}}）$=（ ）
| A． | $-\frac{1}{4}$ | B． | $-\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
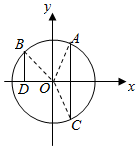（理） 如图，在平面直角坐标系xoy中，点A（x1，y1），B（x2，y2）在单位圆上，∠xOA=α，$α∈（\frac{π}{6}，\frac{π}{2}）$，$∠AOB=\frac{π}{3}$．
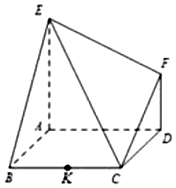如图，已知多面体EABCDF的底面ABCD是边长为2的正方形，EA⊥底面ABCD，FD∥EA，且$FD=\frac{1}{2}EA=1$．