题目内容

设向量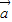=（a1，a2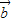），=（b2，b2），定义一种向量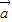?=（a1，a2）?（b1，b2）=（a1b2，a2b2）．已知，点，（x，y）在y=sin x的图象上运动，点Q在y=f（x）的图象上运动且满足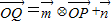（其中O为坐标原点），则y=f（x）的最大值为（ ）
A．1
B．3
C．5
D．
【答案】分析：根据新定义求出向量的坐标，然后将Q的坐标代入y=f（x），从而可求出f（x）的解析式，最后求出最大值即可．
解答：解：由题意可知=（x，sinx），，
根据新定义可知=（2x，）+=（2x+，）
而点Q在y=f（x）的图象上运动
∴f（2x+）=则f（x）=sin（）
∴y=f（x）的最大值为
故选D．
点评：本题主要考查了平面向量的坐标运算，以及函数最值的应用，同时考查了运算求解的能力，属于中档题．
练习册系列答案
相关题目
请先阅读：
设平面向量
a
=（a1，a2），
b
=（b1，b2），且
a
与
b
的夹角为θ，
因为
a
•
b
=|
a
||
b
|cosθ，
所以
a
•
b
≤|
a
||
b
|．
即a1b1+a2b2≤
a
2
1
+
a
2
2
×
b
2
1
+
b
2
2
，
当且仅当θ=0时，等号成立．
（I）利用上述想法（或其他方法），结合空间向量，证明：对于任意a1，a2，a3，b1，b2，b3∈R，都有(a1b1+a2b2+a3b3)2≤(
a
2
1
+
a
2
2
+
a
2
3
)(
b
2
1
+
b
2
2
+
b
2
3
)成立；
（II）试求函数y=
x
+
2x-2
+
8-3x
的最大值．
（2012•烟台二模）设向量
a
=（a1，a2），
b
=（b2，b2），定义一种向量
a
?
b
=（a1，a2）?（b1，b2）=（a1b2，a2b2）．已知
m
=(2，
1
2
)，
n
=(
π
3
，0)，点，（x，y）在y=sin x的图象上运动，点Q在y=f（x）的图象上运动且满足
OQ
=
m
?
OP
+
n
（其中O为坐标原点），则y=f（x）的最大值为（　　）
（2013•门头沟区一模）设向量
a
=（a1，a2），
b
=（b1，b2），定义一种向量积：
a
?
b
=（a1，a2）?（b1，b2）=（a1b1，a2b2）．已知
m
=（
1
2
，3），
n
=（
π
6
，0），点P在y=sinx的图象上运动，点Q在y=f（x）的图象上运动，且满足
OQ
=
m
?
OP
+
n
（其中O为坐标原点），则y=f（x）的最大值是
3
3
．

设向量a＝(a1，a2)，b＝(b2，b2)，定义一种向量．已知点，(x，y)在y＝sinx的图象上运动，点Q在y＝f(x)的图象上运动且满足(其中O为坐标原点)，则y＝f(x)的最大值为

[　　]

A．1

B．3

C．5

D．
设向量
a
=（a1，a2），
b
=（b1，b2），定义一种向量积：
a
?
b
=（a1，a2）?（b1，b2）=（a1b1，a2b2）．已知
m
=（
1
2
，3），
n
=（
π
6
，0），点P在y=sinx的图象上运动，点Q在y=f（x）的图象上运动，且满足
OQ
=
m
?
OP
+
n
（其中O为坐标原点），则y=f（x）的最大值是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网