题目内容
在数列xn中,
=
+
(n≥2),且x2=
,x4=
,则x10等于( )
| 2 |
| xn |
| 1 |
| xn-1 |
| 1 |
| xn+1 |
| 2 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:
=
+
(n≥2),知x3=
=
,由此知x10=
.
| 2 |
| xn |
| 1 |
| xn-1 |
| 1 |
| xn+1 |
| 1 |
| 2 |
| 2 |
| 4 |
| 2 |
| 11 |
解答:解:∵在数列xn中,
=
+
(n≥2),且x2=
,x4=
,
根据等差中项的定义可知,数列{
}是等差数列,
∴当n=3时,
=
+
,x3=
=
,所以公差d=
-
=2-
=
,
所以
=
+8d=
+8×
=
,所以x10=
.
故选A.
或者利用归纳推理判断,x2=
,x3=
=
,x4=
,…猜测xn=
.
故x10=
.
故选A.
| 2 |
| xn |
| 1 |
| xn-1 |
| 1 |
| xn+1 |
| 2 |
| 3 |
| 2 |
| 5 |
根据等差中项的定义可知,数列{
| 1 |
| xn |
∴当n=3时,
| 2 |
| x3 |
| 1 | ||
|
| 1 | ||
|
| 1 |
| 2 |
| 2 |
| 4 |
| 1 |
| x3 |
| 1 |
| x2 |
| 3 |
| 2 |
| 1 |
| 2 |
所以
| 1 |
| x10 |
| 1 |
| x2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
| 2 |
| 11 |
故选A.
或者利用归纳推理判断,x2=
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 5 |
| 2 |
| n+1 |
故x10=
| 2 |
| 11 |
故选A.
点评:本题考查数列的递推式,解题时要注意总结规律.

练习册系列答案
相关题目
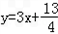 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以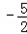 为首项,﹣1为公差的等差数列{xn}.
为首项,﹣1为公差的等差数列{xn}.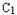 ,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求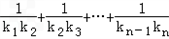 ;
;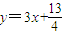 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以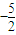 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.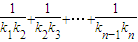 ;
;