题目内容
如图A是单位圆与x轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），| OQ |
| OA |
| OP |
| OA |
| OP |
分析：由已知我们可得：
•
+S=cosθ+sinθ，转化为正弦型函数，结合（0＜θ＜π），从而可求出
•
+S的最大值及此时θ的值．
| OA |
| OP |
| OA |
| OP |
解答：解：
=（1，0），
=（cosθ，sinθ）
∴
•
+S=cosθ+sinθ=
sin(θ+
)(0＜θ＜π)
故
•
+S的最大值是
，
此时θ=
．
故选B．
| OA |
| OP |
∴
| OA |
| OP |
| 2 |
| π |
| 4 |
故
| OA |
| OP |
| 2 |
此时θ=
| π |
| 4 |
故选B．
点评：本题主要考查了向量在几何中的应用，以及利用辅助角公式求最值，同时考查了转化的思想，属于中档题．
练习册系列答案
相关题目
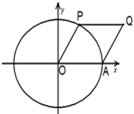如图A是单位圆与x轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），
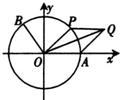（2013•泸州一模）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且
如图A是单位圆与x轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），
，四边形OAQP的面积为S，当
取得最大值时θ的值为
，四边形OAQP的面积为S，当
取得最大值时θ的值为（ ）
