题目内容
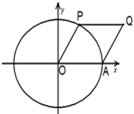如图A是单位圆与x轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），| OQ |
| OA |
| OP |
| OA |
| OP |
分析：根据向量的加法法则得到四边形OAQP为平行四边形，因此算出其面积S=
•
sin∠POA=sinθ．由向量数量积的公式，算出
•
=cosθ，从而得到
•
+S=cosθ+sinθ=
sin（θ+
），再利用正弦函数的图象与性质，即可算出答案．
| |OA| |
| |OP| |
| OA |
| OP |
| OA |
| OP |
| 2 |
| π |
| 4 |
解答：解：∵
=
+
，
∴四边形OAQP为平行四边形，其面积S=
•
sin∠POA，
∵P、A在单位圆上，可得
=
=1，∠AOP=θ，
∴S=
•
sin∠POA=sinθ．
又∵
•
=
•
cos∠POA=cosθ，
∴
•
+S=cosθ+sinθ=
sin（θ+
）
∵0＜θ＜π，可得θ+
∈（
，
）．
∴当且仅当θ+
=
时，即θ=
时，
•
+S=
sin（θ+
）有最大值
．
故选：C
| OQ |
| OA |
| OP |
∴四边形OAQP为平行四边形，其面积S=
| |OA| |
| |OP| |
∵P、A在单位圆上，可得
| |OA| |
| |OP| |
∴S=
| |OA| |
| |OP| |
又∵
| OA |
| OP |
| |OA| |
| |OP| |
∴
| OA |
| OP |
| 2 |
| π |
| 4 |
∵0＜θ＜π，可得θ+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴当且仅当θ+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| OA |
| OP |
| 2 |
| π |
| 4 |
| 2 |
故选：C
点评：本题给出单位圆中的向量与平行四边形，求
•
+S的最大值和相应的角θ的值．着重考查了向量的加法法则、平行四边形的面积计算、三角恒等变换与三角函数的最值求法等知识，属于中档题．
| OA |
| OP |
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
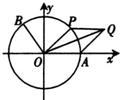（2013•泸州一模）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且
如图A是单位圆与x轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），
如图A是单位圆与x轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），
，四边形OAQP的面积为S，当
取得最大值时θ的值为
，四边形OAQP的面积为S，当
取得最大值时θ的值为（ ）
