Question

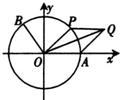（2013•泸州一模）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-

3

5

，

4

5

)，∠AOB=α．
（Ⅰ）求

4cosα-2sinα

5cosα+3sinα

的值；
（Ⅱ）设平行四边形OAQP的面积为S，∠AOP=θ（0＜θ＜π），f（θ）=（cosθ+S）S，求f（θ）的最大值及此时θ的值．

Answer 1

分析：（I）由∠AOB=α可得α的终边与单位圆交于点B(-

3

5

，

4

5

) ，根据三角函数的定义，可求出α的正切值，进而利用弦化切技巧可求出

4cosα-2sinα

5cosα+3sinα

的值；
（Ⅱ）由四边形OAQP为平行四边形可得S_OAQP=2S_△AOP=sinθ，进而可得f（θ）=

2

2

sin（2θ-

π

4

）+

1

2

，结合正弦函数的图象和性质，可得函数的最大值．

解答：解：（I）∵∠AOB=α
∴α的终边与单位圆交于点B(-

3

5

，

4

5

) ，
∴tanα=

4 5

- 3 5

=-

4

3

∴

4cosα-2sinα

5cosα+3sinα

=

4-2tanα

5+3tanα

=

4+ 8 3

5-4

=

20

3

（II）∵四边形OAQP为平行四边形
∴S_OAQP=2S_△AOP=sinθ
∴f（θ）=（cosθ+S）S=sinθ•cosθ+cos²θ=

1

2

sin2θ-

1

2

cosθ+

1

2

=

2

2

sin（2θ-

π

4

）+

1

2

∵0＜θ＜π
∴当θ=

3π

8

时，f（θ）取最大值

2

2

+

1

2

点评：本题考查的知识点是任意角的三角函数的定义，同角三角函数的基本关系，三角函数的最值，熟练掌握三角函数的定义及性质是解答的关键．