题目内容
14.若x,y∈R,且x=$\sqrt{1-y2}$,则$\frac{y+2}{x+1}$的取值范围是[$\frac{3}{4}$,3].分析 x=$\sqrt{1-{y}^{2}}$.可得图象:设$\frac{y+2}{x+1}$=k>0,则化为:kx-y+k-2=0,可得kPB≤k≤kPA.
解答 解:x=$\sqrt{1-{y}^{2}}$.可得图象: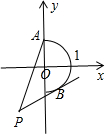
设$\frac{y+2}{x+1}$=k>0,
则化为:kx-y+k-2=0,
由$\frac{|k-2|}{\sqrt{{k}^{2}+1}}≤$1,解得k≥$\frac{3}{4}$.
P(-1,-2),A(0,1).
又kPA=$\frac{1-(-2)}{0-(-1)}$=3.
∴$\frac{3}{4}≤k≤3$.
∴$\frac{y+2}{x+1}$的取值范围是:[$\frac{3}{4}$,3].
故答案为:[$\frac{3}{4}$,3].
点评 本题考查了直线与圆的位置关系、点到直线的距离公式、斜率的意义及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若角120°的终边上有一点(-4,a),则a的值是( )
| A. | $4\sqrt{3}$ | B. | $-4\sqrt{3}$ | C. | $±4\sqrt{3}$ | D. | $\sqrt{3}$ |
2.已知数列{an}的通项公式为an=n-7$\sqrt{n}$+2,则此数列中数值最小的项是( )
| A. | 第10项 | B. | 第11项 | C. | 第12项 | D. | 第13项 |
9. 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点为F1,F2,P是椭圆上一点,M在PF1上,$\overrightarrow{{F}_{1}M}$=2$\overrightarrow{MP}$,PO⊥F2M.则椭圆离心率e的取值范围是( )
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点为F1,F2,P是椭圆上一点,M在PF1上,$\overrightarrow{{F}_{1}M}$=2$\overrightarrow{MP}$,PO⊥F2M.则椭圆离心率e的取值范围是( )
 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点为F1,F2,P是椭圆上一点,M在PF1上,$\overrightarrow{{F}_{1}M}$=2$\overrightarrow{MP}$,PO⊥F2M.则椭圆离心率e的取值范围是( )
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点为F1,F2,P是椭圆上一点,M在PF1上,$\overrightarrow{{F}_{1}M}$=2$\overrightarrow{MP}$,PO⊥F2M.则椭圆离心率e的取值范围是( )| A. | $({0,\frac{{\sqrt{2}}}{2}})$ | B. | $({\frac{{\sqrt{2}}}{2},1})$ | C. | $({0,\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
3.已知集合A={-1,i}为虚数单位,则下列选项正确的是( )
| A. | |-i|∈A | B. | $\frac{1}{i}∈A$ | C. | i3∈A | D. | $\frac{1+i}{1-i}∈A$ |
4.已知抛物线y2=2px(p>0)的准线和圆x2+y2+6x+8=0相切,则实数p=( )
| A. | p=4 | B. | p=8 | C. | p=4或p=8 | D. | p=2或p=4 |